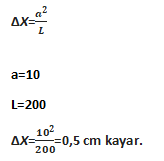AĞIRLIK MERKEZİ
Ağırlık, bir cisme etki eden yerçekimi kuvvetine denir.
G=m.g
G:Ağırlık
m:kütle
g: yerçekimi ivmesi
Ağırlık merkezi ise cismin ağırlığının uygulama noktasıdır.
Başka bir deyişle ağırlık merkezi, cismin bileşkesinin yeridir.
Ağırlık merkezi kütle merkezi olarak ifade edilebilir.
Çekim alanının olmadığı bir alanda sadece kütle merkezinden söz edilebilir.
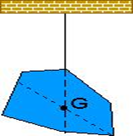
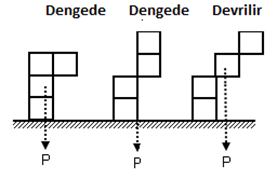
TÜRDEŞ HOMOJEN: cismin her yerinin aynı maddeden yapıldığını ifade eder.
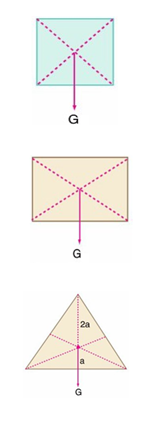
Bir cismin ve bir sistemin ağırlık merkezi bulunurken;
Parça 1 BOYUTLU ise: G= özkütle x çevre(ya da uzunluk)
Parça 2 BOYUTLU ise: G= özkütle x alan
Parça 3 BOYUTLU ise: G= özkütle x hacim
ÖRNEK:
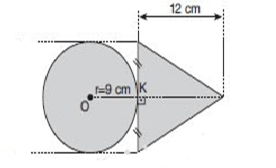
Aynı metalden yapılmış yukarıdaki levhalarla kurulu sistemin ağırlık merkezinin O noktasına olan uzaklığı kaç cm dir? (π=3)
ÇÖZÜM:
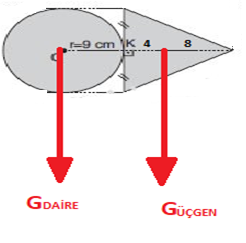
GDAİRE=πr2=243
Güçgen=taban.h/2 =108
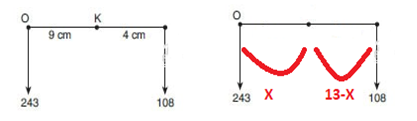
243. X =108.(13-X)
X=4 cm
ÖRNEK:
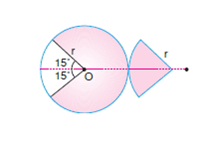
Türdeş daire levhanın ağırlık merkezi O noktasıdır. Bu levhanın birkısmı kesilip şekildeki gibi yapıştırılıyor.
Buna göre, yeni şeklin ağırlık merkezi kaç r yer değiştirir?
ÇÖZÜM:
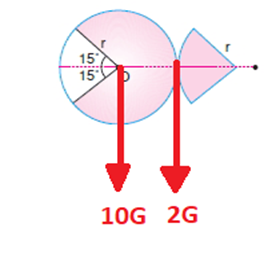
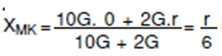
KOORDİNAT DÜZLEMİNDE AĞIRLIK MERKEZİNİN BULUNMASI
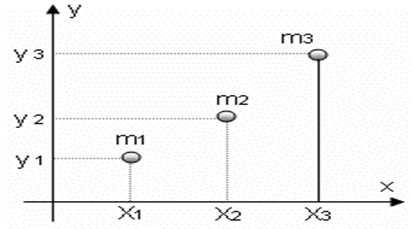
Aynı düzlemde bulunan, birden çok cismin oluşturduğu sistemin kütle merkezinin koordinatları aşağıdaki yöntemle bulunur;
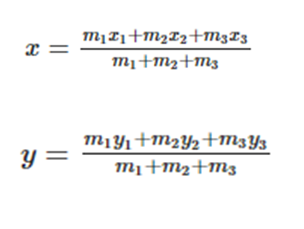
Not:
L uzunluğundaki homojen bir telin ucundan “a” kadarlık parçası kesilerek kendi üzerine katlanırsa:
Ağırlık merkezi,
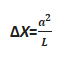
kadar kayar.
Not:
Homojen bir telin bir ucundan a kadarlık kısmı kesilip atılırsa:
Ağırlık merkezi,
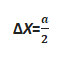
kadar yer değiştirir.
ÖRNEK:
100 cm uzunluğunda bir telin bir ucundan 20 cm kesilip atılıyor.
Cismin ağırlık merkezi kaç cm kayar?
ÇÖZÜM:
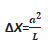
a=20
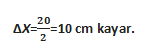
ÖRNEK:
200 cm uzunluğunda bir telin bir ucundan 10cm kesilip üzerine katlanıyor.
Cismin ağırlık merkezi kaç cm kayar?
ÇÖZÜM: