Asal Çarpanlara Ayırma 

Bir doğal sayıyı asal sayıların çarpımı şeklinde yazmaya asal çarpanlara ayırma denir. Bir doğal sayıyı asal çarpanlarına ayırmak için çarpan ağacı veya bölen listesi kullanılır.

Örnek 180 sayısını asal çarpanlarına ayıralım. 

Örnek 

30 sayısını asal çarpanlarına ayıralım.

Bir Sayının Tam Bölenleri 

a, b, c  birbirinden farklı asal sayılar ve k, l, m birer tam sayı olmak üzere,  

A = ak x bl x cm  ifadesi  A sayısının asal çarpanlarının kuvveti biçimde yazılmış halidir.

• A'yı tam bölen asal sayılar a,b,c 'dir.
• A nın pozitif tam bölenlerinin  sayısı;

        (k+1) . (l+1) . (m+1) dir.

• A nın negatif tam bölenleri pozitif tam bölenlerin ters işaretlileridir. Bu sebeple A nın negatif tam bölenlerinin sayısı pozitif tam bölenlerinin sayısına eşittir

(k+1) . (l+1) . (m+1) dir.

• A nın tam sayı bölenlerinin sayısı, pozitif ve negatif tam bölen sayılarının toplamı kadardır.

        2 . (k + 1) . (l + 1) . (m + 1) dir.

EBOB – EKOK EN BÜYÜK ORTAK BÖLEN (EBOB) 

Bir sayı, iki farklı doğal sayının böleni ise, buna doğal sayıların ortak böleni denir. İki ya da daha fazla sayma sayısının ortak bölenleri arasında en büyük olanına, bu sayıların en büyük ortak böleni denir. Verilen sayıları aynı anda bölen asal sayıların çarpımı bu sayıların EBOB unu verir. İki veya daha fazla doğal sayının EBOB u bu sayıların ortak asal çarpanlarının her birine, ayrı ayrı bölünür.

EN KÜÇÜK ORTAK KAT (EKOK) 

Bir sayı iki farklı doğal sayının katı ise, buna doğal sayıların ortak katı denir. İki ya da daha fazla sayma sayısının ortak katları kümesinin en küçük elemanına, bu sayıların en küçük ortak katı denir ve EKOK biçiminde gösterilir. İki sayma sayısının çarpımı, bu sayıların EBOB u ile EKOK unun çarpımına eşittir. Fakat ikiden fazla pozitif tam sayının çarpımı, bu sayıların EBOB u ile EKOK unun çarpımına eşit olmayabilir. 

• A x B = EBOB(A; B) x EKOK(A; B) olur.
• A ve B aralarında asal pozitif doğal sayılar ise 
•  

EBOB (A,B)= 1 ve EKOK (A,B)= A.B

• A ve B sayma sayıları ve A < B olmak üzere EBOB(A; B)< A < B <EKOK(A; B) şeklindedir.
• Ardışık tek sayılar aralarında asaldır.

ÖRNEKLER 

1.  18 ve 24 sayılarının EBOB unu bulalım. 

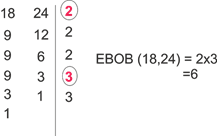
2. 30 ve 9 sayılarının EKOK unu bulalım. 

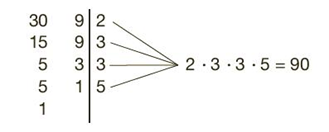
3. Aynı anda aynı yerden hareket eden üç gemiden birincisi 5 gün, ikincisi 7 gün, üçüncüsü 9 günde bir sefere çıkıyor. Bu gemiler kaç gün sonra hep birlikte sefere çıkarlar? 

Çözüm : 

Bu üç geminin ilk kez kaç gün sonra karşılaşacağını bulmak için 5, 7 ve 9'un Ekok' u bulunur. Bu üç sayı aralarında asal sayılar olduğu için birbiri ile çarparakta en küçük ortak katları hesaplanabilir. Ekok (5, 7, 9) = 315 Bu üç gemi 315 gün sonra karşılaşarak hep birlikte sefere çıkarlar. 

4. Bir sepetteki portakallar dörder, beşer ve altışar sayıldığında her seferinde 2 portakal artıyor. Bu sepette en az kaç tane portakal vardır?

 Çözüm: İlk önce 4, 5 ve 6 sayılarının en küçük ortak katı bulunur. EKOK(4, 5, 6) = 2 x 2 x 3 x 5 = 60 Her seferinde 2 portakal arttığına göre sepette; 60 + 2 = 62 tane portakal vardır.

5. Ayrıt uzunlukları 60 cm, 84 cm ve 108 cm olan dikdörtgenler prizması şeklindeki tahta blok eşit küpler halinde kesilecektir. Bu kesim işlemiyle en az kaç küp blok oluşur? 

Çözüm: EBOB ( 60, 84 ,108 ) = 12 60 cm’ lik ayrıt 60 / 12 = 5 parça 84 cm’ lik ayrıt 84 / 12 = 7 parça 108 cm’lik parça 108 / 12 = 9 parça 5 . 7. 9 = 315 küp olur.