Birinci Dereceden Bir Bilinmeyenli Denklemler
a ve b reel sayılar ve a≠0 olmak üzere; ax+b = 0
denklemine birinci dereceden bir bilinmeyenli denklem denir. Denklemin değişkeni yani bilinmeyeni x’tir ve x’in kuvveti 1 olduğu için birinci dereceden adını alır.
Bu denklemde x=-b/a dır.
Bu denklemde Ç.K= dır.
** Denklem çözülürken bilinmeyenler yok oluyor ise kalan eşitliğine bakılır. Kalan eşitlik doğru ise çözüm kümesi gerçek sayılardır, yanlış ise boş kümedir.

a ve b reel sayılar ve a≠0 olmak üzere ax+b=0 denkleminde ;
→a ≠0 için çözüm kümesi 1 elemanlıdır.
→a=0 ve b ≠0 için çözüm kümesi 0 (sıfır) elemanlıdır(boş kümedir ).
→a =0 ve b=0 için çözüm kümesi sonsuz elemanlıdır( ℝ sayılar kümesidir )

a,b ve c reel sayılar ve a≠0 ve b≠0 olmak üzere
ax+by+c=0
denklemine birinci dereceden iki bilinmeyenli denklem denir.
Bilinmeyenler x ve y dir. Çözüm kümesi sıralı ikililerden oluşur. (x,y) Çözüm kümesinin sonsuz elemanlı olması için a=0 ve b=0 olması gerekir.
a,b,c,d,e,f∈ R olmak üzere
ax+by+c=0
dx+ey+f=0
ifadesine birinci dereceden iki bilinmeyenli denklem sistemi denir.
Denklemde verilen iki bilinmeyenden bir tanesi yalnız bırakılarak diğer denklemde yerine yazılır ve bilinmeyen değerler bulunur.
Örnek: y=2x+5
x+y=20 ise x değeri kaçtır?
Çözüm
2.denklemde y=20-x elde edilir ve 1.denklemde yerine yazılır.
20-x=2x+5 olur. Buradan x değeri 5 olarak bulunur.
x+y=20 eşitliğinde x yerine 5 yazılırsa y değeri de 15 olarak bulunur.
Verilen iki denklemdeki bilinmeyenlerden biri seçilip katsayıları mutlak değerce eşit olan zıt işaretli iki sayıya dönüştürülür. Taraf tarafa toplanarak biri yok edilir. Diğer bilinmeyen bulunur. Bulunan bilinmeyen yerine yazılıp diğer bilinmeyen bulunur.
Örnek:
2x+y=12
y-x=9 olduğuna göre x ve y değerlerini bulunuz.
Çözüm x i yok etmek için ikinci denklem 2 ile çarpılır
2x+y=12 2y-2x=18 denklemleri elde edilir.
Taraf tarafa toplama yapıldığında (2x-2x) ten 0 gelecek.
3y=30 olur.
Buradan y=10 bulunur.
2x+y=12 denkleminde yerine yazılırsa x=1 olarak bulunur.
Grafik Temsili
ax+by+c=0 şeklindeki birinci dereceden iki bilinmeyenli her denklem, koordinat düzleminde bir doğru belirtir.
Örnek
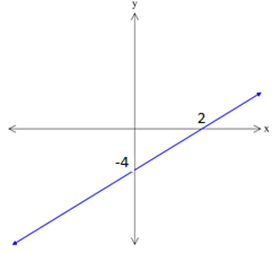
2x-y=4 denkleminin grafiğini çizelim.
x=0 için y= -4 bulunur. y = -4 noktası grafiğin y eksenin kestiği noktadır.
y=0 için x= 2 bulunur. x= 2 noktası grafiğin x eksenin kestiği noktadır.
Grafik
a,b,c,d,e,f∈ R olmak üzere
d₁:ax+by+c=0 d₂: dx+ey+f=0 denkleminin çözümü için üç durum vardır.
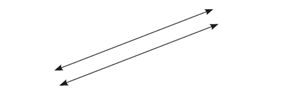
1. : a/d = b/ec/f ise doğrular birbirine paraleldir ve paralel iki doğrunun kesişim noktası olmadığından sistemin çözüm kümesi boş kümedir.
2. : a/d = b/e =c/f ise doğrular çakışıktır ve iki doğru sonsuz noktada kesişir. Çözüm kümesi reel sayılardır.

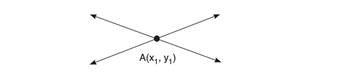
3. : a/d ≠ b/e ise doğrular kesişir ve kesişen iki doğru bir noktada kesiştiğinden çözüm kümesi tek elemanlıdır.
Örnek:
(a-1)x+6y+3=0
ax+3y+4=0
denklem sisteminin çözüm kümesi boş küme olduğuna göre a değeri kaçtır?
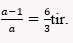
Buradan 3a-3=6a gelir. Denklem çözülürse a= -1 olarak bulunur.
