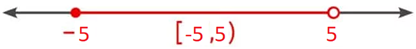> (büyüktür), ≥ (büyüktür veya eşittir), < (küçüktür), ≤ (küçüktür veya eşittir) sembolleri ile yazılan matematiksel ifadelere eşitsizlik denir.

Gerçel (reel) sayı ekseninde (sayı doğrusu) herhangi bir sayının sağında bulunan sayılar daima o sayıdan büyük, solunda bulunan sayılar da o sayıdan küçüktür.
2. Basit Eşitsizliklerin Özellikleri a , b , c , x , y ∈ R olmak üzere;
c < 0 ise , a . c >b .c 'dir.
1. Bir eşitsizliğin her iki tarafına aynı sayı eklenir ya da çıkarılırsa eşitsizlik yön değiştirmez. 2 < x < 5 → 2 + 3 < x + 3 < 5 + 3→ 5 < x + 3 < 8 dir. 2 < x < 5 → 2 - 3 < x - 3 < 5 - 3→ -1 < x - 3 < 2 dir.
2. Bir eşitsizliği pozitif bir sayı ile çarparsak (bölersek) eşitsizlik yön değiştirmez; negatif bir sayı ile çarparsak (bölersek) eşitsizlik yön değiştirir. -4 < x < 1 → 7/ -4 < x < 1 → -28 < 7x < 7 dir. -4 < x < 1 → 7/ -4 < x < 1 → -1 < 7x < 28 dir.
3. Aynı yönlü eşitsizlikler taraf tarafa toplanabilir.
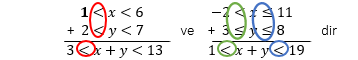
4. Aynı yönlü eşitsizlikler taraf tarafa çıkartılamaz. Bu durumda eşitsizliklerden biri (-) ile çarpılarak toplamaya dönüştürülür. Aşağıdaki eşitsizliklere göre x - y değerini bulmak için y'nin bulunduğu eşitsizlik (-) ile çarpılır.
2 < x < 5
7 < y < 12 ( -12 < -y < -7 ) Daha sonra x + (-y) hesaplanır.
2 < x < 5
-12 < -y < -7
+-------------------------
-10 < x - y < -2 dir.
5. Aynı yönlü eşitsizlikler taraf tarafa çarpılamaz. Bu durumda eşitsizliklerin uç noktaları ikişerli olarak birbiri ile çarpılır. Bu işlemler sonucunda en büyük değer ve en küçük değer alınır.
2 < x < 5 2 . 1 = 2 5 . 1 = 5
-4 < x < 1 2 . -4 = -8 5 . -4 = -20 → -20 < -8 < 2 < 5 olup
*------------------
-20 <x .y< 5 dir.
Sayı Doğrusunda Gösterme
ÖRNEK: 2x − 5>−15 eşitsizliğini çözelim ve çözüm kümesini sayı doğrusunda gösterelim.
2x − 5 > −15
2x > −10
x> −5
x değerleri -5 ten büyüktür.
Yani çözüm kümesi (−5,∞) olarak bulunur.

ÖRNEK: −14 ≤ 3x + 1 < 16 eşitsizliğini çözelim ve çözüm kümesini sayı doğrusunda gösterelim.
−14 ≤ 3x + 1 < 16
−15 ≤ 3x < 15
−5 ≤ x < 5 Çözüm kümesi [−5,5) olarak bulunur.