ÇEMBERDE UZUNLUK
Özellikler
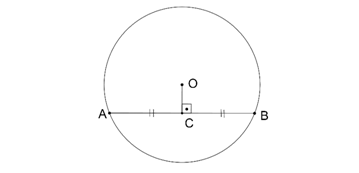
1. Bir çemberde merkezden kirişe çizilen dikme, kirişi ortalar.
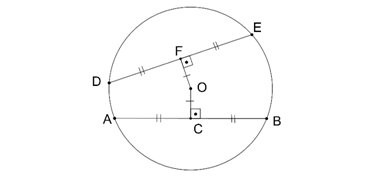
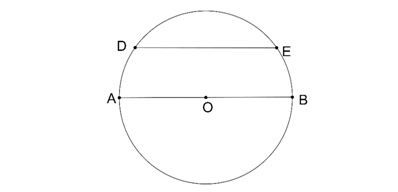
2.Çemberin merkezinden eşit uzaklıktaki kirişlerin uzunlukları eşittir.
|OF|=|OC|
|AB|=|DE|
3.Çemberde eşit uzunluktaki kirişlerin ayırdığı yayların ölçüleri eşittir.
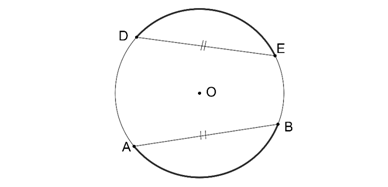
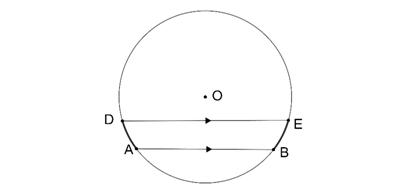
4.Paralel kirişlerin arasında kalan yayların ölçüleri eşittir.
5.Merkeze daha yakın kiriş daha uzundur. En uzun kiriş çaptır.
6.Bir çember içindeki bir P noktasından geçen en kısa kiriş P noktasından geçen çapa dik olan kiriştir.
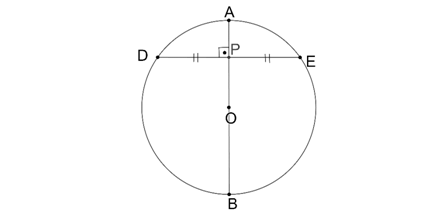
7. |PA|=|PB|
[OP] açıortay
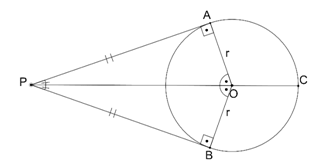
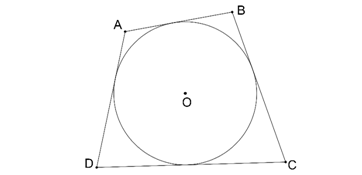
8.Teğetler Dörtgeni:
|AB|+|DC|=|BC|+|AD| ve
|AB|+|DC|=|BC|+|AD|=u ise
Alan(ABCD)=u.r dir.
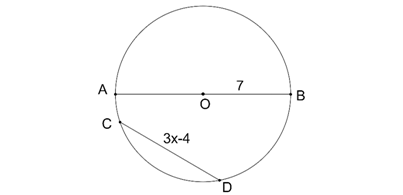
Örnek 1
Şekilde verilen [AB] çaplı çembere göre x’in alabileceği en büyük tam sayı değeri kaçtır?
|CD|<|AB| olması gerektiğinden
3x-4<14
3x<18
x<6 olup x’in alabileceği en büyük tam sayı 7 dir.
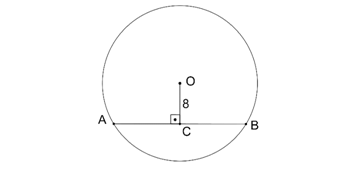
Örnek 2
Şekilde verilen O merkezli çemberde
|OC|=8 br
|AB|=12 br
olduğuna göre çemberin yarıçapı kaç birimdir?
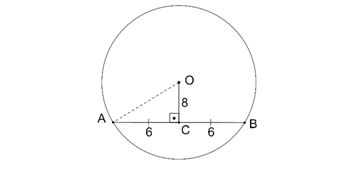
|AC|=|CB|=6 br olur.
AOC dik üçgeninde pisagor bağıntısından
6-8-10 üçgeni bulunur.
yarıçap |OA|=10 br’dir.
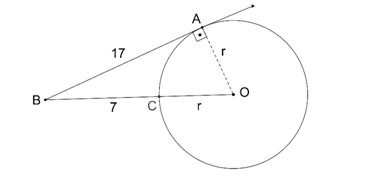
Örnek 3
Şekilde verilen O merkezli çemberde
[BA teğet |AB|=17 |BC|=7 br
olduğuna göre çemberin çapı kaç birimdir?
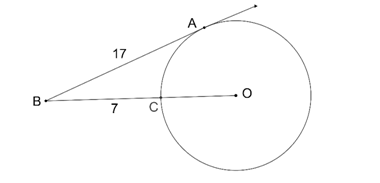
[OA]⊥[AB] çizilirse, |OA|=|OC|=r olur. ABO üçgeninde pisagor bağıntısından
r^2+〖(7+r)〗^2=〖17〗^2 r=8 Çap istendiğinden 8.2=16 br bulunur.