Çokgenler - TYT AYT 2023 (YKS 2023) Uzaktan Eğitim

Bir düzlemde birbirinden farklı ve herhangi üçü doğrusal olmayan A1, A2, A3, … gibi n tane (n ³ 3) noktayı ikişer ikişer birleştiren doğru parçalarının oluşturduğu kapalı şekillere çokgen denir.
a. İçbükey (konkav) çokgenler: Bir çokgenin bazı kenar doğruları çokgeni kesiyorsa bu tür çokgenlere İçbükey çokgen denir.

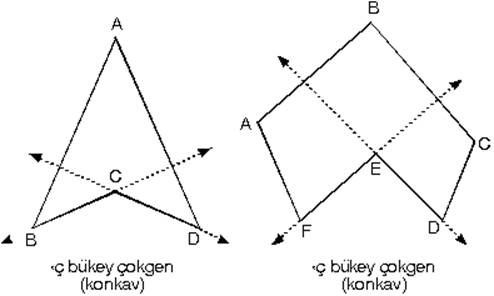b. Dışbükey (konveks) çokgenler: Kenar doğrularının hiçbiri, çokgeni kesmiyorsa bu çokgenlere dışbükey çokgen denir.

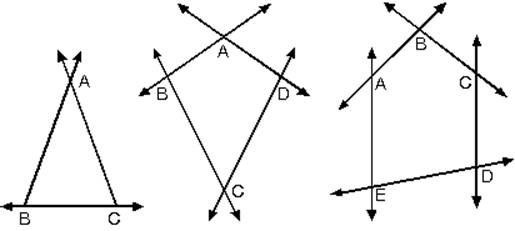c. Çokgenlerin elemanları

A, B, C, D, E noktalarına çokgenin köşeleri denir. Komşu iki köşeyi birleştiren [AB], [BC], [CD], [DE] ve [EA] doğru parçaları çokgenin kenarlarıdır.

İç bölgede kenarlar arasında oluşan açılara çokgenin iç açıları denir.
İç açılara komşu ve bütünler olan açılara çokgenin dış açıları denir.
Köşeleri birleştiren kenarlar haricindeki doğru parçalarına köşegen adı verilir.

2. Dışbükey Çokgenlerin Özellikleri
a. İç açılar toplamı: Dış bükey bir çokgenin n tane kenarı var ise iç açılarının toplamı

(n - 2).180°

Üçgen için (3 – 2) . 180° = 180°
Dörtgen için (4 – 2) . 180° = 360°
Beşgen için (5 – 2) . 180° = 540°
b. Dış açılar toplamı: Bütün dışbükey çokgenlerde,

Dış açılar toplamı=360°

c. Köşegenlerin sayısı: n kenarlı dışbükey bir çokgenin

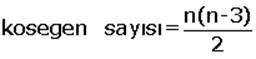Bir köşeden (n – 3) tane köşegen çizilebilir.

n kenarlı dışbükey bir çokgenin içerisinde, bir köşeden köşegenler çizilerek (n – 2) adet üçgen elde edilebilir.

3. Düzgün Çokgenler
Bütün kenarlarının uzunlukları eşit ve bütün açılarının ölçüleri eşit olan çokgenlere düzgün çokgen denir.

a. Şekildeki düzgün altıgende olduğu gibi düzgün çokgenlerin köşelerinden daima bir çember geçer. Bu çembere çevrel çember denir.

b. Düzgün çokgenlerde eşit sayıda kenarı birleştiren köşegenler birbirine eşittir.

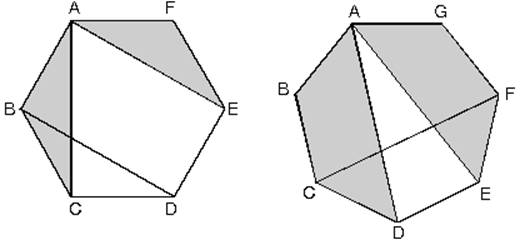|AC|=|AE|=|BD| |AD|=|AD|=||

c. Kenar sayısı çift olan düzgün çokgenlerde karşılıklı kenarlar paraleldir.

[AF] // [CD], [AB] // [ED]....[AH] // [DE], [AB] // [FE]...

d. Kenar sayısı tek olan düzgün çokgenlerde karşı kenara çizilen dik karşı kenarı ortalar. Köşeden kenarın ortasına çizilen doğru parçası kenara diktir şeklinde de ifade edilir.

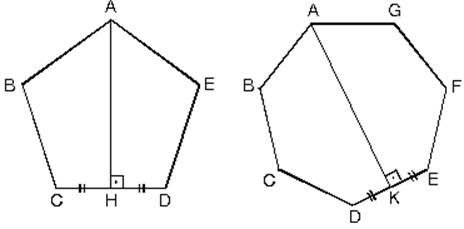e. n kenarlı düzgün bir çokgende

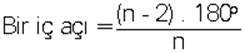f. Konveks çokgenlerin dış açıları toplamı 360° olduğundan düzgün çokgenin bir dış açısı

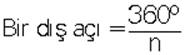4. Düzgün Çokgenin Alanı

a. n kenarlı düzgün çokgenin bir kenarı a ve iç teğet yarıçapı r ise alanı

b.n kenarlı bir düzgün çokgende bir kenarı gören merkez açı

(Bu açı aynı zamanda dış açıdır) ve çevrel çemberin yarıçapı R ise çokgenin alanı

Düzgün altıgen altı tane eşkenar üçgenden oluşur.

Bir kenarına a dersek

DÖRTGENLERİN GENEL ÖZELLİKLERİ

1. Bir dörtgende komşu iki iç açının açıortaylarının oluşturduğu açının ölçüsü, diğer iki açının ölçüleri toplamının yarısına eşittir.

2. Bir dörtgende karşı iki açının açıortayları arasındaki dar açının ölçüsü diğer iki açının ölçüleri farkının mutlak değerinin yarısına eşittir.

3. Köşegenleri ve köşegenlerinin arasındaki açısının ölçüsü bilinen dörtgenin alanı;
ABCD dörtgeninde [AC] ve [BD] köşegen uzunlukları ile α biliniyor

Köşegenleri birbirine dik olan dörtgenlerde
(sin 90° = 1 olduğundan)

Köşegen doğruları birbirine dik ise

4. Köşegenleri ve köşegenlerinin arasındaki açısının ölçüsü bilinen içbükey dörtgenin alanı;
[AC] ve [BD] köşegenleri ile köşegen doğruları arasındaki a biliniyor ise ABCD içbükey dörtgeninin alanı;

5. Köşegenleri dik kesişen dörtgenlerin kenarları arasındaki bağıntı;

ABCD dörtgeninde [AC] ^ [BD]

Köşegenleri dik olan dörtgenlerin karşılıklı kenarlarının kareleri toplamı eşittir.

Köşegenleri dik içbükey dörtgenlerde de karşılıklı kenarların kareleri toplamı eşittir.

ABCD dörtgeninde

6. Dörtgenlerde köşegenlerin ayırdığı alanlar; ABE ve ADE üçgenlerinin yükseklikleri eşit olduğundan alanlarının oranı tabanlarının oranına eşittir.

7. Dörtgenlerde kenarların orta noktalarının birleştirilmesiyle oluşan paralelkenar; ABCD dörtgeninde kenarların orta noktaları birleştirilerek oluşan KLMN dörtgeni paralelkenardır. Paralelkenarın alanı dörtgenin alanının yarısına eşittir.
[KL] // [BD] // [MN] ve |KL| = |MN| =
[LM] // [AC] // [KN] ve |LM| = |KN| =