IŞIK DALGALARINDA KIRINIM VE GİRİŞİM OLAYLARI
ÇİFT YARIKTA GİRİŞİM DENEYİ
( YOUNG DENEYİ )
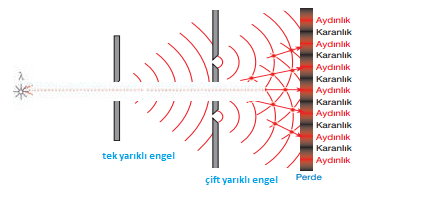
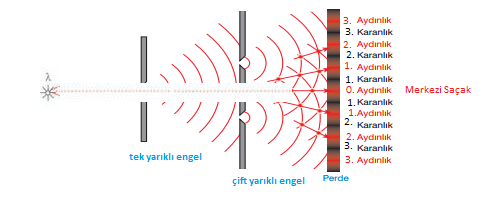
Su dalgalarında gözlenen girişim olayındaki katar ve düğüm çizgilerine karşılık olarak, ışık dalgalarında bir perde üzerinde aydınlık ve karanlık çizgiler gözlenmiştir. Işık bilindiği üzere hem dalga hem de parçacık özelliği gösterir. Kırınım ve girişim olayları ışığın yalnızca dalga özelliği ile açıklanabilir.
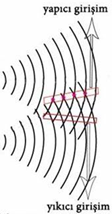
Tepe noktalarının kesiştiği noktalar çift tepe noktalarıdır, yapıcı girişim oluştururlar. Çukur noktalarının kesiştiği noktalar çift çukur noktalarıdır, yapıcı girişim oluştururlar. Tepe ve çukur noktalarının kesiştiği noktalar ise söndürücü girişim oluştururlar.
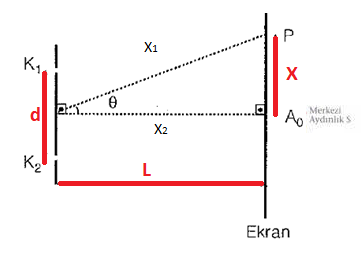
Perde üzerinde herhangi bir P noktasının yeri Perde üzerinde herhangi bir P noktasının yerini yol farkı belirler.
∆S= X1 – X2 ∆S: Yol farkı
Aydınlık Şartı
P noktası için yol farkı tam değerde ise P n. aydınlık saçak üzerindedir.
∆S= n.λ
Karanlık Şartı
P noktası için yol farkı buçuklu değerde ise P n. karanlık saçak üzerindedir.
∆S=( n- ½ ).λ
Özel Durumlar
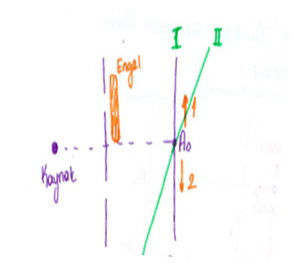
ENGEL SAYDAM İSE; engelden gelen ışınlar gecikmeye uğrar ve A0 1 yönünde kayar.
ENGEL SAYDAM DEĞİLSE; yarık genişliği küçülür, saçak aralıkları büyür ve A0 2 yönünde kayar.
PERDE I KONUMUNDAN II KONUMUNA GETİRİLİRSE: 1 konumundaki saçakların genişliği artar 2 konumundaki saçakların genişliği azalır.
TEK YARIK DENEYİ
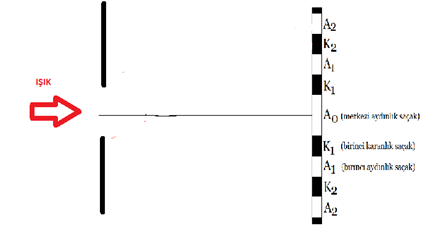
Tek renkli ışık demeti dar bir yarıktan geçtiğinde kırınıma uğrayarak ekran üzerinde aydınlık ve karanlık girişim saçakları oluşturur.

A0 dan uzaklaştıkça saçakların parlaklığı azalır.
Yol Farkı(∆S)
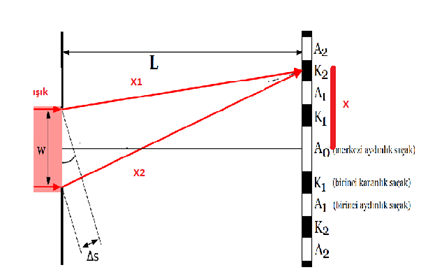
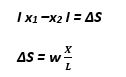
Saçak Aralığı
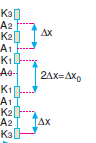
Tek yarık deneyinde merkezi aydınlık saçak genişliği diğer saçakların iki katıdır.
Merkezi aydınlık saçak dışındaki saçakların tümünün genişliği aynıdır.
Aydınlık saçakların %85 ini merkezi aydınlık saçak oluşturur.
∆X : Saçak aralığı
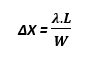
Özel Durumlar
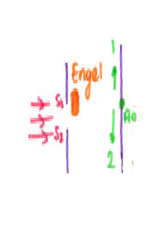
ENGEL SAYDAM İSE; saçak aralıkları değişmez ve A0 1 yönünde kayar.
ENGEL SAYDAM DEĞİLSE; yarık genişliği küçülür, saçak aralıkları büyür ve A0 2 yönünde kayar.