FONKSİYONLAR A ≠ Ø ve B ≠ Ø olmak üzere, A dan B ye bir β bağıntısı verilmiş olsun. A’nın her elemanı B’nin elemanlarıyla bir ve yalnız bir kere eşleniyorsa bu bağıntıya fonksiyon denir. x∈ A ve y ∈ B olmak üzere, A’dan B’ye bir f fonksiyonu f: A → B ya da x → f(x) = y biçiminde gösterilir. A’ya fonksiyonun tanım kümesi, B ye de değer kümesi denir.

Fonksiyonlarda İşlemler
A ∩ B = Ø olmak üzere,
f: A → B ve g: B → R fonksiyonları tanımlansın.
Fonksiyon Çeşitleri
Birebir Fonksiyon
Bir fonksiyonun tanım kümesindeki her elemanın görüntüsü farklı ise fonksiyona birebir(1-1) fonksiyon denir.

Örten Fonksiyon
Görüntü kümesi değer kümesine eşit olan fonksiyonlara örten fonksiyon denir.
f: A → B f(A) = B ise , f örtendir.
m! = m . (m - 1) . (m - 2). ... . 3 . 2 . 1 dir.
İçine Fonksiyon
A’dan B’ye tanımlı f fonksiyonunda değer kümesinde açıkta eleman kalıyor ise, fonksiyona içine fonksiyon denir.
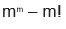
Birim Fonksiyon
Her elemanı kendisine eşleyen fonksiyona birim fonksiyon denir.
f: R→ R, f(x) = x Genelde I ile gösterilir.
Sabit Fonksiyon
Tanım kümesindeki bütün elemanları değer küme-sindeki bir elemana eşleyen fonksiyona sabit fonksiyon denir.
Çift ve Tek Fonksiyon
f: R→ R;
f(–x) = f(x) ise, f fonksiyonu çift fonksiyondur.
f(–x) = –f(x) ise, f fonksiyonu tek fonksiyondur.
Eşit Fonksiyon
f: A → B
g: A → B
Her x ∈ A için f(x) = g(x) ise, f fonksiyonu g fonksiyonuna eşittir.
Doğrusal Fonksiyon

Permütasyon Fonksiyon
f: A → A olmak üzere, f fonksiyonu bire bir ve örten ise, f fonksiyonunapermütasyon fonksiyon denir.
A = olmak üzere, f: A → A
f = fonksiyonu permütasyon fonksiyon olup;
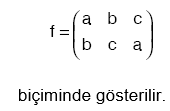
Ters Fonksiyon
f: A → B, f = bire bir ve örten fonksiyon olmak üzere,
f−1 : B → A , f−1 = fonksiyonuna f’nin ters fonksiyonu denir.
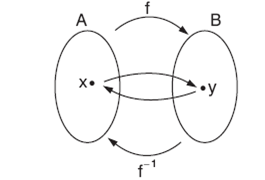
(x,y) ∈ f ise , ( y , x ) ∈ f−1 olduğu için, y = f(x) ise, x = f−1(y)'dir. Ayrıca (f−1)−1 = f'dir.


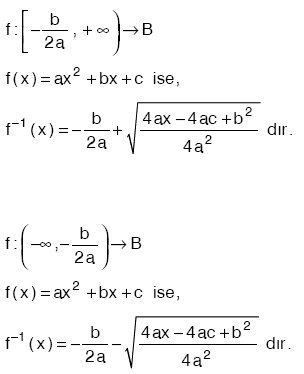
Bileşke Fonksiyon
f: A → B, g: B → C fonksiyonları tanımlansın.
f ve g’yi kullanarak A kümesinin elemanlarını C kümesinin elemanlarına eşleyen fonksiyona g ile f’nin bileşke fonksiyonu denir.
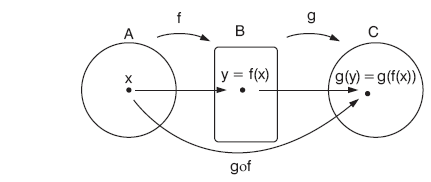
(fog)oh = fo(goh) = fogoh olur.
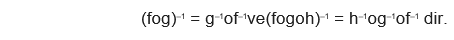
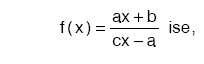
Grafikte Değer Okuma
Fonksiyonun elemanlarına analitik düzlemde karşılık gelen noktaların görüntüsü fonksiyonun grafiğini oluşturur.
Örnek
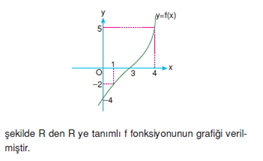
Buna göre f(3)+f(1)-f(0)+f(4) işleminin sonucu kaçtır?
f(3)=0
f(1)=-2
f(0)=-4
f(4)=5 0+(-2)-(-4)+5=7 bulunur.