İKİNCİ DERECEDEN DENKLEMLER
a, b, c gerçel sayı ve ≠ olmak üzere;
ax² + bx + c = 0
biçimindeki ifadeye ikinci dereceden bir bilinmeyenli denklem denir.
Bu denklemi sağlayan x sayılarına denklemin kökleri; tüm köklerin oluşturduğu kümeye denklemin çözüm kümesi; a,b,c sayılarına da denklemin katsayıları denir.
İkinci Dereceden Denklemlerin Çözüm Kümesinin Bulunuşu
1) Çarpanlara Ayırma Yöntemi
ax² + bx + c = 0 denklemi f(x) . g(x) = 0 şeklinde yazılabiliyorsa f(x) = 0 veya g(x) = 0 dır.
2) Diskriminant (Δ) Yöntemi
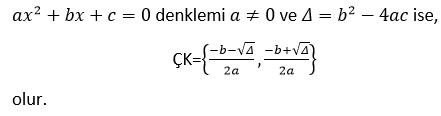

x1 = x2 = - b/2a
Bu köklere eşit iki kök, çakışık kök ya da çift katlı kök denir.
1) b = 0 ve a ≠ 0 dır.
2) Bu kökler gerçel ise, b = 0 , a ≠ 0 ve a.c ≤ 0 dır.
Kökler ve Katsayılar Arasındaki Bağıntılar

Kökleri Verilen İkinci Dereceden Denklemin Yazılması

ax² + bx + c = 0 ve dx² + ex + f = 0 denklemlerinin çözüm kümesi aynı ise,
a/d = b/e = c/f dir.
ÇÖZÜMLÜ ÖRNEKLER
1) x² + 12x + 3m - 6 = 0 denkleminin kökleri eşit olduğuna göre, m değeri kaçtır?


3) x² - 2x + n = 0 denkleminin kökleri x² - nx + 2 = 0 denkleminin köklerinden birer fazla olduğuna göre, m değeri kaçtır?
