Kütle Çekim Yasası Kütlesi olan her cisim birbirine bir çekme kuvveti uygular.
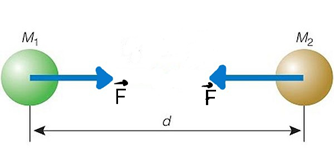
Newton bu kuvvetin büyüklüğünün cisimlerin kütleleri ile doğru, merkezleri arasındaki mesafenin karesi ile ters orantılı olduğunu ortaya koymuştur.
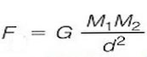
Eşitlikte yer alan "G " gravitasyon sabiti olup, değeri 6,67 × 10 -11 N. m2 / kg2 dir.
İki cismin birbirine uyguladığı kuvvet daima eşit büyüklükte ve zıt yönlüdür.
Kütle Çekim Alanı
Kütleye sahip her varlığın bir kütle çekim alanı vardır. Gezegenlerde kütle çekim alanından dolayı çevresinde ve üzerindeki cisimlere kütle çekim kuvveti uygular. Bu kuvvet etkisiyle cisim kütle çekim ivmesi kazanır. Dünyanın Kütle Çekim İvmesi Dünyanın kütle çekim kuvveti etkisiyle çevresinde ve yüzeyinde bulunan cisimlere kazandırdığı ivmeye yer çekimi ivmesi denir.
Dünya yüzeyindeki bir cisim için;
Fnet=m . a G.(MD. Mc)/d2= Mc.a = G MD/d2
Yer çekimi içmesi g ile sembolize edilir.
g= G.MD/d2
Yer çekim ivmesi birimi m/s2 dir.
Dünyanın çekim ivmesi dünyanın özkütlesi (d) bağlı olarak hesaplanmak istenirse
g= G.4/3. π. R . d bağıntısı kullanılır.
Yer çekim ivmesinin Dünyanın merkezine olan uzaklığa bağlı olarak değişimi aşağıda görülen grafikteki gibidir.
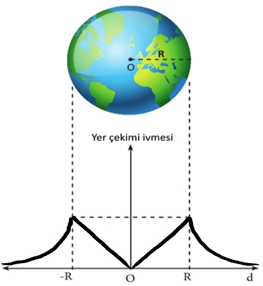
Önemli: Dünyanın şekli kutuplardan basık olduğu için kutuplardan ekvatora gidildikçe yer çekimi ivmesi azalır.
Kütle Çekim Potansiyel Enerjisi Bir cisim üzerine etkiyen kütle çekim kuvvetinin büyüklüğü ile kitleler arası uzaklığın çarpımı kütle çekim potansiyel enerjiyi vermektedir. Kütle çekim potansiyel enerji kütleler arası mesafe ile doğru orantılıdır.
Bağlanma Enerjisi Kütle çekim kuvveti etkisindeki cisimler den birinin bulunduğu konumdaki toplam enerjisine denir.
Kurtulma Enerjisi Kütle çekim etkisindeki cisimlerden birinin kütle çekim kuvvetinin etkisinden kurtulması için verilmesi gereken en küçük enerjiye denir.
Dünya çevresinde dolanan uydu için;
yörüngede sahip olduğu enerji uydunun bağlanma enerjisi, uydunun Dünya'nın çekim etkisinden kurtulabilmesi için uyduya verilmesi gereken en küçük enerji kurtulma enerjisidir.
KEPLER YASALARI Johannas Kepler tarafından gezegenlerin hareketi üç yasa ile açıklanmıştır.
1.Yasa (Yörüngeler Yasası) Gezegenler, odaklarının birinde Güneş bulunan eliptik bir yörüngede dolanım yaparlar.

2. Yasa (Alanlar Yasası)
Güneş etrafında dolanan bir gezegeni Güneşe bağlayan çizgi eşit zaman aralıklarında eşit alanlar tarar.
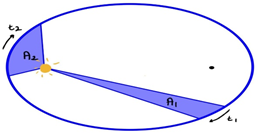
A1 / A2 = t1 / t2
3. Yasa (Periyotlar Yasası) Bir gezegenin yörüngesel periyodunun karesi ile dolandığı elipsin ortalama yarı çapının küpünün oranı daima sabittir
. T2 / Rortalama3 = K
K =3,367 × 1018m3 / s2
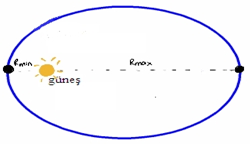
Rmax: Gezegenin güneşe en uzak olduğu mesafe
Rmin: Gezegenin güneşe en yakın olduğu mesafe
Rortalama= (Rmin + Rmax)/ 2