LİMİT
x değişkeni a sayısına a dan küçük değerlerle yaklaşıyorsa bu yaklaşmalara soldan yaklaşma denir ve

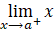
ile gösterilir. x değişkeni a sayısına a dan büyük değerle yaklaşıyorsa bu yaklaşmalara sağdan yaklaşma denir ve  ile gösterilir.  Bir fonksiyonun limitinin olması için saldan limit ve sağdan limit birbirine eşit olmalıdır. Eğer soldan limit ile sağdan limit birbirine eşit değil ise o noktada limit yok denir.

Şeklinde gösterilir.
SÜREKLİLİK
Bir fonksiyonun limitinin olması için sağdan ve soldan limitinin birbirine eşit olması gerekir. Sürekli olması için soldan limit, sağdan limitin eşit olmasının yanında o noktadaki limitin de eşit olması gerekir.

şartı sağlandığında  fonksiyonu süreklidir.
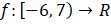
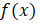
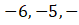
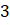
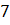
ÖRNEK: Aşağıda verilen  tanımlı fonksiyonun grafiği verilmiştir. Buna göre2,  ve  noktaları için limitini ve sürekliliğini inceleyelim.

ÇÖZÜM:

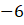
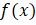
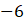
 noktası sınır değeri olduğundan sadece sağdan limitine bakılır. Sınır değerinde limit vardır. Sürekli olması için o noktada da limiti, sağdan limite eşit olmalıdır. Eşit olduğundan süreklidir. Öyleyse  fonksiyonu  noktasında süreklidir ve limiti  dir.

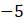
Eşitliği sağlandığından  noktasında hem limitli hem de süreklidir.


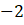
 noktasında sağdan ve soldan limiti eşit olduğunda limiti var ama  noktasındaki limit değeri sağdan ve soldan değeri eşit olmadığından sürekli değildir.

3 noktasında soldan limit ve sağdan limit birbirine eşit olmadığından 3 noktasında limiti yoktur. Eğer bir noktada limit yoksa o noktada fonksiyon sürekli değildir.

Sınır noktası olduğundan sadece soldan limite bakılır ve sınır noktasında limiti vardır. Soldan limiti ve o noktadaki limiti birbirine eşit olmadığından 7 noktasında sürekli değildir.