LOGARİTMİK DENKLEMLER
Logaritma denklemleri çözerken aşağıdaki kurallara göre denklemler çözülür.
i) 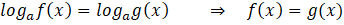
ii)
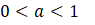
için

iii)
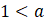
için
 ÖRNEK:
ÖRNEK: 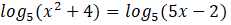
denkleminin çözüm kümesini bulalım.
ÇÖZÜM: Tabanlar eşit olduğundan
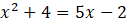
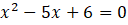
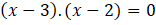
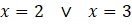
Bulunan değerler logaritma fonksiyonunu tanımsız yapıp yapmadığı yerine koyularak denenmelidir. Tanımsız yapan değerler çözüm kümesinin elemanı olamaz. Burada bulduğumuz değerler logaritma fonksiyonlarımızı tanımsız yapmadığından
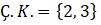
olarak bulunur.
ÖRNEK: 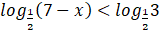
olduğuna göre, çözüm kümesini bulalım.
ÇÖZÜM: Tabanlar eşit ve
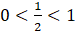
olduğundan eşitsizlik yön değiştirecektir.
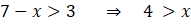
olur. Ayrıca logaritma fonksiyonun tanımlı olması için
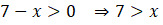
olur. İki eşitsizliğin ortak kesişim kümesini aldığımızda
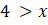
olur.
ÖRNEK: 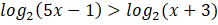
denkleminin çözüm kümesini bulalım.
ÇÖZÜM: Tabanda bulunan sayı 2 ve
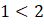
olduğundan eşitsizlik yön değiştirmeyecektir.
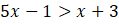
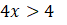
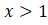
logaritma fonksiyonunun tanımından ayrıca
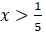
ve
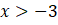
olarak bulunur. Kümelerin kesişimini aldığımızda

olarak sonuç bulunur.
ÖRNEK: 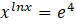
denkleminin kökler çarpımını bulalım.
ÇÖZÜM: Her tarafta
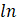
alalım.
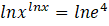
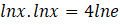
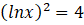
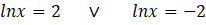
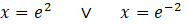
bulunur. Kökler çarpımı
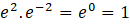
olarak bulunur.