MUTLAK DEĞER
A. Tanım
Bir x sayısının başlangıç noktasına olan uzaklığına mutlak değer denir. Bu |x| ile gösterilir.
x, x > 0 ise,
|x| = 0, x = 0 ise,
-x, x < 0 ise,
Dikkat: |x| ifadesinin alabileceği en küçük değer 0 dır.
B. Mutlak Değerin Özellikleri
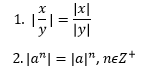
3. |x| = |-x|
4. |x - y| = |y - x|
5. |a . b| = |a| . |b|
6. a > 0 olmak üzere, |x| = a ise , x = a ya da x = -a dır.
7. |f(x)| = |g(x)| ise , f(x) = g(x) ya da f(x) = -g(x) dir.
8. |x| + |y| = 0 ise, x=0 ve y=0 dır.
C. Mutlak Değerli Denklemler
c>0 olmak üzere,
1. |x| = c ise, x = c ya da x = -c dir.
2. |ax + b| = c ise, ax + b = c ya da ax + b = -c dir.
3. |ax + b| + |dx + e| = c olsun. c'nin alabileceği en küçük değeri bulmak için mutlak değerli ifadeleri yapan değerler teker teker denenir. Yani x = -b / a ve x = -e / d için denenir.
4. a / |ax + b| + |dx + e| = c olsun. c'nin alabileceği en büyük değer için paydanın alacağı en küçük değer bulunur.
5. |ax + b| = dx + e olsun. Denklemin çözüm kümesini bulmak için;
a. ax + b = dx + e ve
b. ax + b = -dx - e için çözüm kümeleri bulunur. Bu çözüm kümelerinde, dx + e ifadesini negatif yapan değerler çıkartılır.
6. |ax + b| = |dx + e| olsun. Denklemin çözüm kümesini bulmak için
a. ax + b = dx + e ve
b. ax + b = -dx - e denklemlerinin çözüm kümelerine eşittir.
NOT: Bu denklemlerin çözümünü tablo kullanarak çözebiliriz.
Bilgi: Mutlak değerli ifadeyi 0 yapan noktalara kritik noktalar denir.
Örnek:
|2x - 6| + |x + 2| = 10 olsun. Bu denklemin çözüm kümesini bulunuz.
2x - 6 = 0 ise , x = 3 tür.
x +2 = 0 ise , x = -2 dir. Bu noktalar dikkate alınarak işaret incelemesi yapılır.
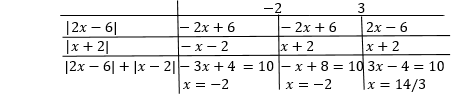
Ç.K. = elde edilir.
D. Mutlak Değerli Eşitsizlikler
a ≥ 0 olsun.
a. |x| ≤ a ise , -a ≤ x ≤ a olur.
b. |x| ≥ a ise , x ≥ a ya da x ≤ -a olur.
c. a < x < b ise , a < x < b ya da -b < x < -a olur.
KONU DEĞERLENDİRME SORULARI
Cevap: 11
Burada x = -3 için A = 1 ve x = 3 için A = 11 olur. O halde cevap 11 olur.
2. |8-|x+1|| = 4 denkleminde x in alabileceği değerler toplamı kaçtır?
Cevap: -19
|x+1| = x+1 ya da |x+1| = -x-1 olur.
x+1 için , |8-|x+1|| = |7-x| = 4 olur.Buradan, 7 - x = 4 ya da 7 - x = -4 olup, x = 3 ya da x = 11 olur.
-x -1 için,|8-|x+1|| = |9+x| = 4 olur. Buradan, 9+x = 4 ya da 9+x = -4 olup, x = -5 ya da x = -13 olur.
Böylece, (-13) + (-5) +3 + 11 = -4 elde edilir.
3. |3x-6| < 9 ve x - y = 3 olmak üzere y nin alabileceği tam sayı değerleri nelerdir?
Cevap: -3,-2,-1,0,1
Burada, -9 < 3x - 6 < 9 olup (*) ... -1 < x < 5 elde edilir.
x - y = 3 olduğundan y = x - 3 olur. (*) denkleminden -4 < x - 3 < 2 elde edilir. O halde, y nin alacağı değerler;
-3, -2, -1, 0, 1 dir.