PRİZMALAR
Alt ve üst tabanları paralel ve eş şekillerden oluşan cisimlere prizma denir. Yanal ayrıtları taban düzlemine dik olan prizmalara dik prizma adı verilir.
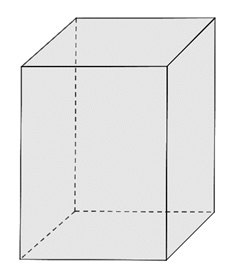
-Köşeleri birleştiren doğru parçalarına ayrıt denir.
[AA’], [BB’], [CC’], [DD’] yanal ayrıtlardır.
-Prizmanın tabanları dışındaki yüzeylere yanal yüzey denir. Yan yüzler dikdörtgendir.
-Prizmalar tabanlarına göre isimlendirilir. Taban kare ise kara prizma, dikdörtgen ise dikdörtgen prizma denir.
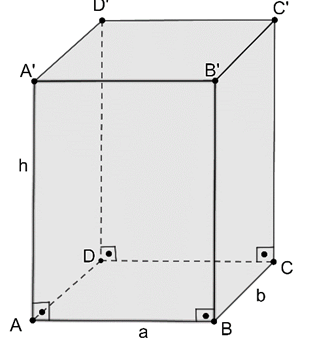
V hacim olmak üzere
V=(Taban Alanı)xYükseklik
Yanal Alan=(Taban Çevresi)xYükseklik
Tüm Alan=Yanal Alan+2.(Taban Alanı)
Dikdörtgen Prizma
Tabanları dikdörtgen olan dik prizmaya denir.
12 ayrıtı, 6 yüzü vardır.
En uzak iki köşeyi birleştiren doğru parçasına cisim köşegeni denir.
|BD’|=f cisim köşegenidir.
|AB|=a |BC|=b ve |CC’|=c olmak üzere
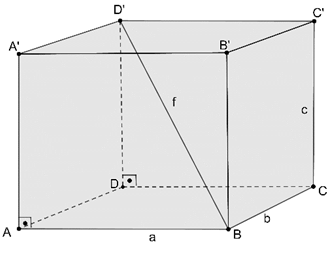
Hacmi=a.b.c
Yanal Alan=2(a+b).c
Tüm Alan=2(ab+ac+bc)
![]()
KÜP
Tüm yüzeyleri eş karelerden oluşan dikdörtgenler prizmasına denir.
Tüm ayrıt uzunlukları eşittir.
|AB|=|BC|=|CC’|=a
|BD’|=f cisim köşegeni
|BD|=e yüzey köşegeni olmak üzere
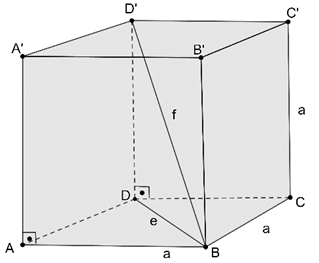
Hacmi=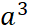
Yanal alan=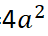
Tüm alan=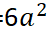
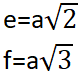
SİLİNDİR
Tabanları eş dairelerden oluşan prizmaya silindir denir. Ana doğruları tabana dik olan silindirlere dik silindir veya dönel silindir, ana doğruları tabana dik olmayan silindirlere eğik silindir denir.
[AA’]: ana doğru
[OO’]=h yükseklik
Dik silindir.
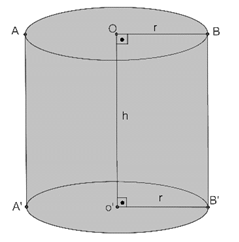
[BH]=h yükseklik
Eğik silindir
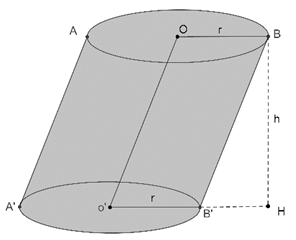
Taban alanı=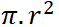
Yanal alanı=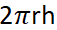
Tüm alan=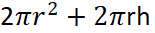
Hacmi=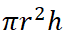
Örnek 1
Şekilde verilen üçgen dik prizmanın yüksekliği 8 br,
|AB|=6 br
|AC|=8 br
olduğuna göre, hacmini ve yüzey alanını bulunuz.
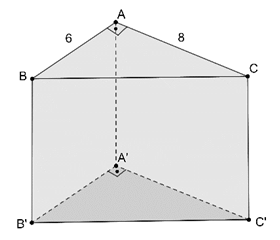
Hacmi=(Taban alanı)x(yükseklik)=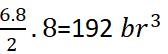
ABC dik üçgeninde Pisagor bağıntısından 6-8-10 üçgeni bulunur. |BC|=10 br
yüzey alanı= Yanal Alan+2.(Taban Alanı)
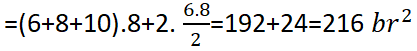 bulunur.
bulunur.
Örnek 2
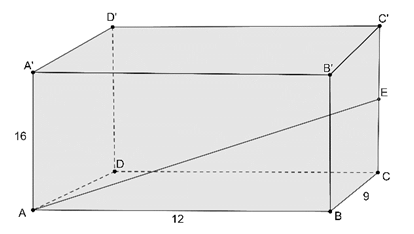
Şekilde verilen dikdörtgen prizmaya göre,
|C’E|=|EC|
|AA’|=16 br
|AB|=12 br
|BC|=9 br
olduğuna göre |AE| kaç birimdir?
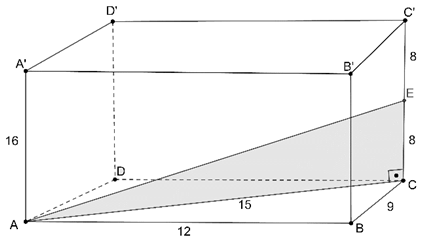
|AA’|=16 oluğundan |C’E|=|EC|=8 olur.
[AC] çizilirse 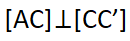 olur.
olur.
ABC dik üçgeninde Pisagor bağıntısından 9-12-15 üçgeni bulunur.
ACE dik üçgeninde Pisagor bağıntısından 8-15-17
|AE|=17 br bulunur.
Örnek 3
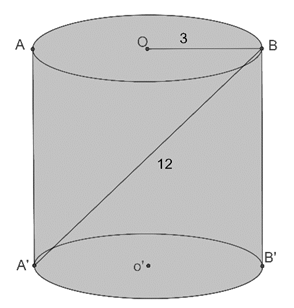
Şekilde verilen dik silindire göre
|OB|=3 br
|A’B|=12 br olduğuna göre
silindirin hacmi kaç birim küptür?
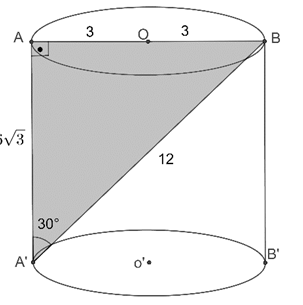
|AO|=|OB|=3 br
AA’B üçgeninde 30-60-90
üçgeninden 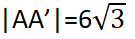 bulunur.
bulunur.
Hacim=(Taban alanı)x(yükseklik)
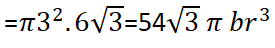 bulunur.
bulunur.