TEMEL KAVRAMLAR VE SAYILAR
A. Rakam ve Sayı
Sayıları ifade etmek için kullanılan sembollere rakam adı verilir.
Örnek: 0,1,2,3,4,5,6,7,8,9 Çokluk belirtecek şeklide, rakamların bir araya getirilmesiyle oluşan ifadelere sayı adı verilir.
Örnek: -8 , 9 , 17 , 2/3 , √41 , π
Not:Her rakam bir sayıdır. Ancak, her sayı bir rakam değildir.
B. Sayı Kümeleri
1. Doğal Sayılar
N = 0,1,2,3,... kümesinin elemanlarının her birine doğal sayı denir.
Dikkat: Sıfır hariç tüm doğal sayılar pozitif doğal sayıdır.
2. Sayma Sayıları N+ = 1,2,3,...kümesinin elemanlarının her birine sayma sayılar (pozitif doğal sayı) denir.
3. Tam Sayılar Z = ... , -2,-1,0,1,2, ... kümesinin elemanlarının her birine tam sayı denir. Burada, Z+ = 1,2,3, ... kümesinin elemanlarının her birine pozitif tam sayı denir. = ... , -3,-2,-1 kümesinin elemanlarının her birine negatif tam sayı denir.

4. Rasyonel Sayılar
b ≠ 0 ve a ile b birer tam sayı olmak üzere a/b şeklinde yazılabilen sayılara rasyonel sayı denir. O halde rasyonel sayılar kümesini Q =(a/b) : a,b∈ Z ve b ≠ 0 olarak ifade edebiliriz.
NOT: Her tam sayı paydası 1 olan bir rasyonel sayıdır.
5. İrrasyonel Sayılar Rasyonel olmayan sayılara irrasyonel sayılar denir. Yani b ≠ 0 ve a ile b birer tam sayı olmak üzere a/b şeklinde yazılamayan sayılardır. Ondalık gösterimlerine bakıldığında ise virgülden sonra belli bir kurala göre gitmeyen sayılardır. Bu sayılar Q' ile gösterilir.
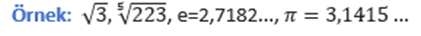
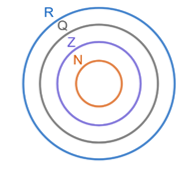
6. Reel ( Gerçek ) Sayılar Rasyonel sayılar kümesiyle irrasyonel sayılar kümesinin birleşimi olan kümeye reel (gerçel) sayılar kümesi denir. Reel sayılar kümesi = R = Q U Q' şeklinde ifade edilebilir. O halde bu bilgilerimizden yola çıkarak aşağıdaki genellemeye ulaşabiliriz.
R: Reel Sayılar Kümesi
Q: Rasyonel Sayılar Kümesi
Z: Tam Sayılar Kümesi
N: Doğal Sayılar Kümesi
C. Sayı Çeşitleri
1. Çift Sayı
n∈ Z olsun. Genel ifadesi 2n olan tam sayılara çift sayıdır. Ç = ... , -2n , ... , -4 , -2 , 0 , 2 , 4 , ... , 2n , ... kümesinin elemanlarının her biri çift sayıdır. Ç bir çift sayı olsun. O halde,
2. Tek Sayı
n∈ Z olsun. Genel ifadesi 2n+ 1 olan tam sayılara tek sayı denir. T = ... , -(2n + 1) , ... , -3 , -1 , 1 , 3 , ... (2n +1) , ...} kümesinin elemanlarının her biri tek sayıdır. K tek sayı olsun. O halde,
T bir tek sayı ve Ç bir çift sayı olsun. O halde,
3. Pozitif Sayı ve Negatif Sayı
Sıfırdan büyük her reel (gerçel) sayı pozitif sayıdır. Sıfırdan küçük her reel (gerçel) sayı ise negatif sayıdır. a,b,c,d∈ R ve a < b < 0 < c < d olmak üzere,
e> ç ise, f pozitif sayıdır. e< ç ise, f negatif sayıdır.
4. Asal Sayı
Kendisinden ve 1 den başka herhangi bir pozitif tam sayıya tam bölünmeyen doğal sayılara asal sayı denir. Örnek: 2, 3, 5, 7, 11, 13, 17, 19
NOT: En küçük asal sayı 2 dir. Ayrıca, 2 den başka çift asal sayı yoktur.
Dikkat: Asal sayıların çarpımı asal değildir. Bilgi:Asal olmayan, 1 den büyük tam sayılara bileşik sayı denir.
5. Aralarında Asal Sayılar
a ve b iki tam sayı olsun. Bu iki sayının 1 den başka ortak böleni yoksa bu sayılara aralarında asal sayılar denir. a ile b aralarında asal ise, aralarındaki oran en sade biçimdedir.
Örnek: 22 ve 39 sayılarının aralarında asal olup olmadıklarını inceleyelim.
22 sayısının bölenleri: 1,2,11,22
39 sayısının bölenleri: 1,3,13.39
Bu iki sayının tek bir ortak böleni vardır da 1 sayısıdır. Böylece 22 ile 39 sayıları aralarında asaldır.
D. Ardışık Sayılar
Belirli bir kural doğrultusunda art arda gelen sayı dizilerine ardışık sayılar denir. n bir tam sayı olsun. O halde,
n, n + 1, n + 2, n + 3 dır.
2n, 2n + 2, 2n + 4, 2n + 6 dır.
2n + 1, 2n + 3, 2n + 5, 2n + 7 dir.
5n, 5n + 5, 5n + 10, 5n + 15 dir.