ÜÇGENDE ALAN
1. Genel Alan Bağıntısı |
|
Bir üçgenin alanı, bir kenarı ile o kenara ait yüksekliğin çarpımının yarısıdır.
 |
Hangi kenarı kullanırsak kullanalım üçgenin alanı sabittir. |
|
Bir ABC üçgeninde yükseklik her zaman üçgenin içinde olmayabilir.
|
|
|
2. Dik Üçgende Alan
|
|
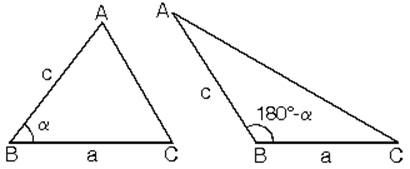
3. Bir açısı ve bu açının kenarları bilinen üçgenin alanı;
ABC üçgeninde m(ABC) = a |AB| = c |BC| = a
|
|
a. Birbirini 180° ye tamamlayan açıların sinüsleri eşit olduğundan;
 |
|
eşitliği vardır. |
b. |BC| = a |AB| = c uzunlukları sabit olan ABC üçgeninin alanının maksimum olabilmesi için a = 90° olmalıdır. |
|
c. Hipotenüs uzunluğu sabit olan ABC dik üçgeninin alanının en büyük değerini alabilmesi için |AB| = |AC| olmalıdır. |
|
4. Üç kenarının uzunluğu verilen üçgenin alanı;
|
|
5. Çevresi ve iç teğet çemberinin yarıçapı verilen üçgenin alanı; ABC üçgeninin iç teğet çemberinin yarıçapı r olsun. |
|
Bu üç alanı toplayarak ABC üçgeninin alanını bulabiliriz.
|
Bir ABC üçgeninde iç teğet çemberin yarıçapı r ve yükseklikler
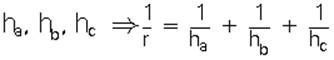
ABC dik üçgeninde A(ABC) = |BD|.|DC| |
|
6. Kenarları ve çevrel çemberinin yarıçapı verilen ABC üçgeninin çevrel çemberinin merkezi O ve yarıçapı R olsun. |
|
Üçgenin kenarının orta noktasından çizilen dik doğrulara orta dikme denir. |
|
O noktası çevrel çemberin merkezidir.
7. Yükseklikleri eşit üçgenlerin alanları arasındaki bağıntı;
Yükseklikleri eşit üçgenlerin alanlarının oranı tabanlarının oranına eşittir.
ABC ve ACD üçgenlerinin tabanları aynı doğru üzerinde ve tepe noktaları aynı noktada olduğuna göre, yükseklikleri eşittir. 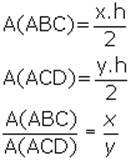 |
|
8. Tabanları eşit üçgenlerin alanlarının oranı yüksekliklerinin oranına eşittir. |
|