BASİT MAKİNELER
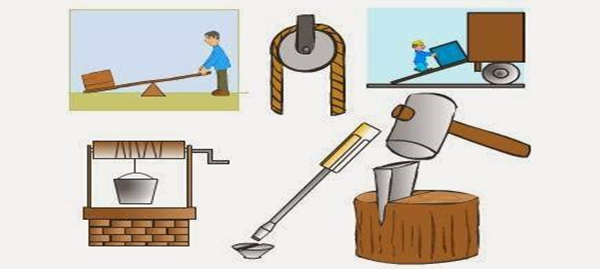
İş kolaylığı sağlamak için geliştirilmiş aletlere basit makine denir.
Basit makinelerde;
Kuvvetkazancı elde edildiğinde yoldan aynı oranda kayıp, yoldan kazanç elde ediliyorsa aynı oranda kuvvetten kayıp olur.
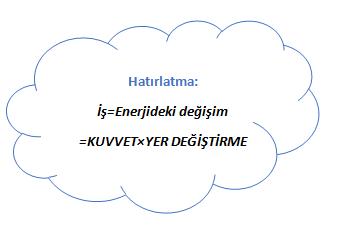
!!!İşten ve enerjiden kazanç ya da kayıp elde edilmez.
KALDIRAÇLAR
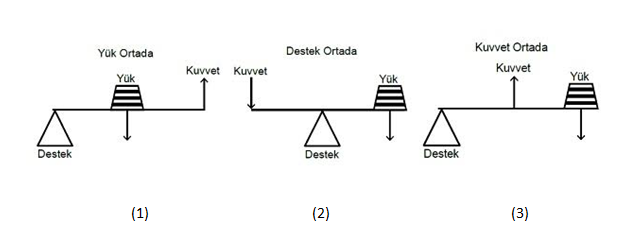
Sabit bir destek etrafında hareket edebilen ve yapacağımız işe göre destek noktasının yeri değişebilen sağlam çubuklara kaldıraç denir.
Uygulanan kuvvetin destek noktasına olan uzaklığına kuvvet kolu yük ile destek arasındaki uzaklığa yük kolu denir.
Kaldıraç ile hesaplamalar yaparkendesteğe göre tork-denge prensibinden faydalanılır.

KASNAKLAR
Kasnaklar arasındaki iletişim kayışla sağlanır. Kasnaklarda kuvvet, birinden diğerine kayışla aktarılır.
Örnek olarak;
Dikiş makineleri,patoz makinası kasnaklara örnek verilebilir.
Farklı Merkezli Kasnaklar
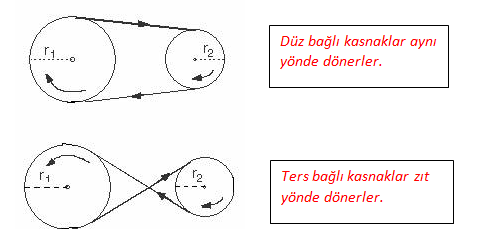
2πr1 . n1 = 2πr2 . n2
r1 . n1 = r2 . n2
Eş Merkezli Kasnaklar

n:tur sayısı
DİŞLİLER
Eş Merkezli Dişliler

Farklı Merkezli Dişliler

2πr1 . n1 = 2πr2 . n2= 2πr3 . n3
r1 . n1 = r2 . n2= r3. n3
n:tur sayısı
NOT: Birbirlerini döndüren dişli ve kasnaklarda dönme sayısı ile yarıçapların çarpımı eşittir.
ÖRNEK:
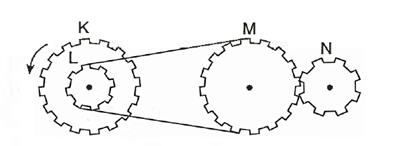
Şekildeki K dişlisi ok yönünde döndürülüyor.
Bu sistemle ilgili aşağıdakilerden hangisi söylenemez?
CEVAP:E
ÇIKRIK
Dönme eksenleri aynı yarıçapları farklı iki silindirin oluşturduğu sisteme çıkrık denir.
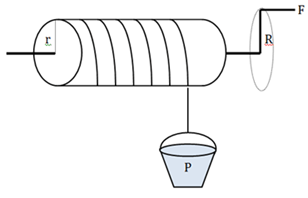
F.2πR = P. 2πr
F. R = P. r
MAKARALAR
SABİT MAKARA
Çevresinden geçen ip çekildiğinde yalnızca dönme hareketi yapabilen makaralara sabit makara denir.
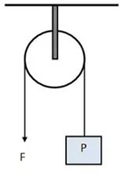
F. r = P. r
F = P
Kuvvetten kazanç yoktur.
Kuvvet h kadar çekilirse ağırlık h kadar yükselir.
HAREKETLİ MAKARA
Çevresinden geçen ip çekildiğinde hem dönebilen hem de yükselip alçalabilen makaralara hareketli makara denir.

2F = P
F=P/2
Ağırlığı ihmal edilen hareketli makarada kuvvetten kazanç vardır. Ağırlığı ihmal edilmiyor ise ağırlığa göre kuvvetten kazanç olabilir de olmayabilir de. Hareketli makarada F kuvveti ile ipin ucu h kadar çekilirse, karşılıklı paralel iplerin herbirinden h/2 kadar kısalma olur ve cisim h/2 kadar yükselir.
ÖRNEK:
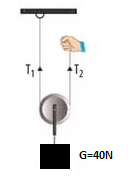
Şekildeki makaranın ağırlığı 10N olup sistem dengede olduğuna göre;
İplerde oluşan gerilmeler T1 ve T2 kaç Newton’dur?
ÇÖZÜM:
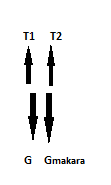
T1 +T2 = G + GmakaraT1 = T2
T1 +T2 = 40+10 T1 = T2= 25 N
PALANGA
Hareketli ve sabit makara gruplarından oluşan sistemlere palanga denir.
Makara ağırlıkları ve sürtünmelerin önemsiz olduğu palanga sistemlerinde, kuvvet ile yük arasındaki ilişki, makaralarda olduğu gibi denge şartlarından bulunur.
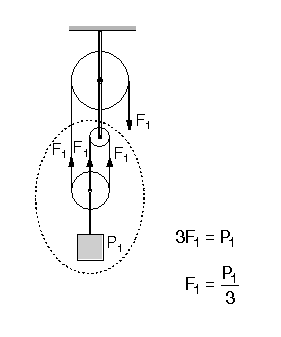
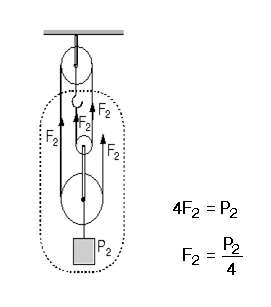
NOT: Kuvvet kazancı;

bağıntısı ile hesaplanır.
VİDA
Vida, iki yüzeyi birbirine birleştirirken, en çok kullanılan, basit makinelerden birisidir. Vidada iki diş arasındaki uzaklığa vida adımı (a) denir.
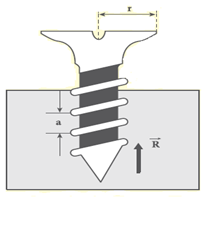
Vida başı bir tam dönüş yaptığında vida, vida adımı (a) kadar yol alır. N kez döndüğünde ise
N. akadar yol alır.
F. 2πr = R. a
ÖRNEK:
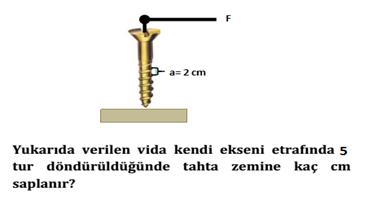
ÇÖZÜM:
Vidanın ilerleme miktarı h=N.a olduğuna göre; 2.5=10cm saplanır.
EĞİK DÜZLEM
Ağır yükleri yukarı çıkarmak için eğik düzlem adı verilen yokuşlardan yararlanılır. Bir levhanın ya da kalasın bir ucu yükün çıkarıldığı yere dayanırsa eğik düzlem elde edilir
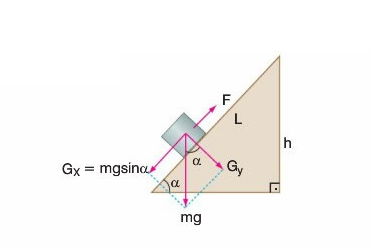
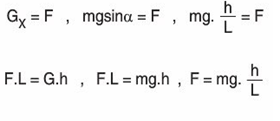
Alınan işin verilen işe oranı, bir makinenin verimi olarak tanımlanır. Yüksek verim, verilen işin çoğunun makine tarafından işe dönüştürülmesi demektir.
Düşük verim, verilen işin bir kısmının kaybolduğunu ve kullanışlı bir işe dönüştürülemediğini gösterir. Verim genellikle yüzde olarak ifade edilir.
Verim yüzdesi = (Alınan iş/Verilen iş ) . 100
Verim yüzdesi = (Ağırlığın yaptığı iş/Kuvvetin yaptığı iş ) . 100
ÖRNEK:
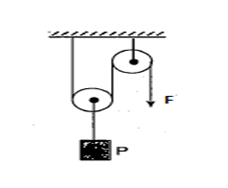
Ağırlığı P= 40 N olan cisim sürtünmesi önemsiz makaralarla kurulu sistemde sabit hızla yükseliyor.
Sistemin verimi %80 olduğuna göre F kaç Newton’dur?
ÇÖZÜM:
Verim yüzdesi = (Ağırlığın yaptığı iş/Kuvvetin yaptığı iş ) . 100
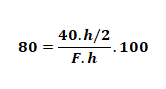
F=25N
ÖRNEK:
Basit makinelerle ilgili aşağıdakilerden hangisi söylenemez?
CEVAP:D