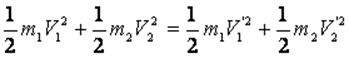
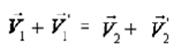
Cisimler, kütle merkezlerini birleştiren doğru üzerinde çarpışarak çarpışma sonrası aynı doğrultuda hareket ederlerse bu çarpışmalara merkezi esnek çarpışmalar denir.

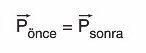
![]()
![]()
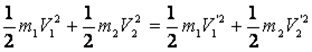
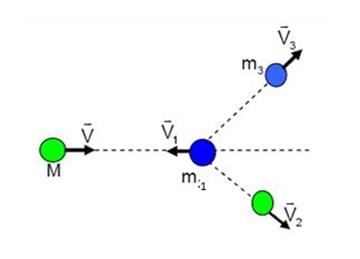
Cisimler, kütle merkezlerini birleştiren doğru üzerinde çarpışmazlarsa bu çarpışma merkezi olmayan çarpışmadır.
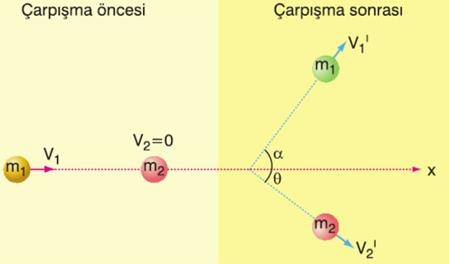
Momentumun vektörel bir nicelik olmasından ötürü yatay ve düşey olmak üzere ayrı ayrı momentum korumu düşünülmelidir.
![]()
Not: Eşit kütleli iki cisim merkezi esnek çarpışma yaparsa; çarpışma sonrası iki cismin hızı birbirine aktarılır. Çarpışma sonrası, 1. cisim 2. cismin çarpışma öncesi hızı ile 2. cisim 1. cismin çarpışma öncesi hızı ile hareket eder.
Not: Momentum büyüklükleri aynı iki cisim merkezi esnek çarpıştıktan sonra cisimler aynı hız büyüklüğü ile yönlerini değiştirerek hareket eder.
ESNEK OLMAYAN ÇARPIŞMALAR
Çarpışan cisimler çarpışma sonrası birlikte hareket ederler.
Yalnız momentum korunur.
![]()
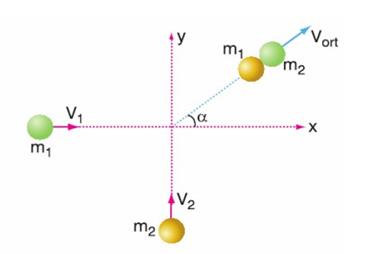
PATLAMALAR
İç patlama geçiren cisimlerde momentum korunur.
![]()
![]()
ÖRNEK:
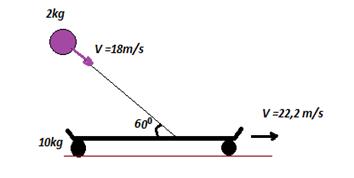
Yukarıdaki şekilde 22,2m /s hızla hareket eden kaykayın üzerine 18m/s hızla top fırlatılıyor. Top kaykayın üzerine yapıştığına göre kaykayın son hızı kaç m/s olur?
ÇÖZÜM:
Yatayda momentum korunumu yazarsak;
![]()
10. (22,2) + 2. (18.0,5) = (10+2).Vortak
222+18=12. Vortak
Vortak = 20 m/s
ÖRNEK:
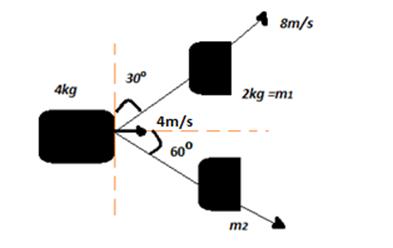
4kg lık cisim havada iç patlama geçirip iki parçaya ayrılıyor. Parçalarının birinin kütlesi ve hızı şekildeki gibi olduğuna göre ikinci parçanın kütlesi ve hızı ne olur?
ÇÖZÜM:
4= m1 + m2 =2+m2
m2=2 kg
Momentum korunum yazarsak;
Düşeyde çarpışma öncesi momentum sıfır olduğundan patlama sonrasında da sıfır olacaktır.
Yatayda ise;

Vektörlerde aralarındaki açı 120⁰ olan eşit vektörlerin toplamının bir vektörün değerine eşitliği göz önünde bulundurularak
2.V2 = 16
V2 = 8 m/s