ÖZEL ÜÇGENLER
DİK ÜÇGEN. Bir açısının ölçüsü 90° olan üçgene dik üçgen denir. Dik üçgende 90° nin karşısındaki kenara hipotenüs, diğer kenarlara dik kenar adı verilir. Hipotenüs üçgenin daima en uzun kenarıdır.
şekilde, m(A) = 90°
[BC] kenarı hipotenüs
[AB] ve [AC] kenarları dik kenarlardır.
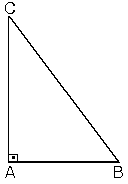
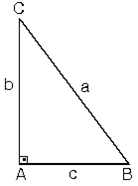
PİSAGOR BAĞINTISI. Dik üçgende dik kenarların uzunluklarının kareleri toplamı hipotenüsün uzunluğunun karesine eşittir. ABC üçgeninde m(A) = 90°
a2=b2+c2
ÖZEL DİK ÜÇGENLER
1. (3 - 4 - 5) Üçgeni. Kenar uzunlukları (3 - 4 - 5) sayıları veya bunların katı olan bütün üçgenler dik üçgendir. (6 - 8 - 10), (9 - 12 - 15), … gibi
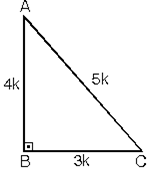
2. (5 - 12 - 13) Üçgeni. Kenar uzunlukları (5 - 12 - 13) sayıları ve bunların katı olan bütün üçgenler dik üçgenlerdir. (10 - 24 - 26), (15 - 36 - 39), … gibi.
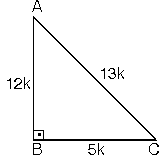
3. (8 - 15 - 17) Üçgeni. Kenar uzunlukları 8, 15, 17 sayıları ile orantılı olan üçgenler dik üçgenlerdir.
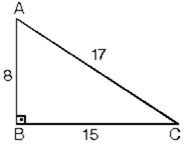
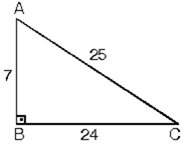
4. (7 - 24 - 25). Kenar uzunlukları 7, 24, 25 sayıları ile orantılı olan üçgenler dik üçgenlerdir.
5. İkizkenar dik üçgen. ABC dik üçgen |AB| = |BC| = a |AC| = a2
m(A) = m(C) = 45° İkizkenar dik üçgende hipotenüs dik kenarların 2 katıdır.
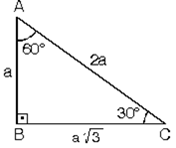
6. (30° – 60° – 90°) Üçgeni. ABC eşkenar üçgeni yükseklikle ikiye bölündüğünde
ABH ve ACH (30° - 60° - 90°) üçgenleri elde edilir.
|AB| = |AC| = a
|BH| = |HC| = a/2
Pisagordan 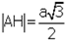
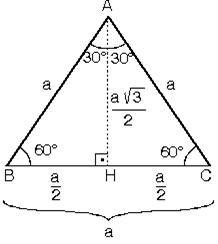
(30° - 60° - 90°) dik üçgeninde; 30°'lik açının karşısındaki kenar hipotenüsün yarısına eşittir. 60°’lik açının karşısındaki kenar, 30° nin karşısındaki kenarın 3 katıdır.
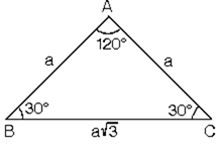
7. (30° - 30° - 120°) Üçgeni. (30° - 30° - 120°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 120° lik açının karşısındaki kenar a3 olur.
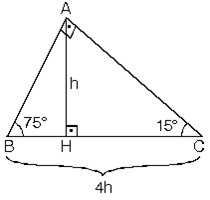
8. (15° - 75° - 90°) Üçgeni. (15° - 75° - 90°) üçgeninde hipotenüse ait yükseklik |AH| = h dersek, hipotenüs |BC| = 4h olur. Hipotenüs kendisine ait yüksekliğin dört katıdır.
ÖKLİT BAĞINTILARI. Dik üçgenlerde hipotenüse ait yüksekliğin verildiği durumlarda benzerlikten kaynaklanan öklit bağıntıları kullanılır.
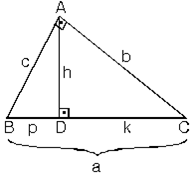
1. Yüksekliğin hipotenüste ayırdığı parçaların çarpımı yüksekliğin karesine eşittir.
h2 = p.k
c2 = p.a
b2 = k.a
2. ABC üçgeninin alanını iki farklı şekilde yazıp eşitlediğimizde
a.h =b.c
Yukarıda anlatılan öklit bağıntıları kullanılarak 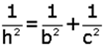 elde edilir.
elde edilir.
Genellikle bu öklit bağıntısını kullanmak yerine, yukarıdaki öklit bağıntıları ve pisagor bağıntısını kullanarak çözüme gideriz.