Doğrusal olmayan üç noktayı birleştiren üç doğru parçasının birleşimine üçgen denir.
[AB] È[AC]È [BC] = ABC üçgenidir. Burada; A, B, C noktaları üçgenin köşeleri, [AB], [AC], [BC] doğru parçaları üçgenin kenarlarıdır. |
|
BAC, ABC ve ACB açıları üçgenin iç açılarıdır. |
|
ABC üçgeni bir düzlemi; üçgenin kendisi, iç bölge, dış bölge, olmak üzere üç bölgeye ayırır. |
|
1. Kenarlarına göre üçgen çeşitleri
a. Çeşitkenar üçgen
Üç kenar uzunlukları da farklı olan üçgenlere denir. |
|
b. ikizkenar Üçgen
Herhangi iki kenar uzunlukları eşit olan üçgenlere denir. |
|
c. Eşkenar Üçgen
Üç kenar uzunlukları da eşit olan üçgenlere denir. |
|
2. Açılarına göre üçgenler
a. Dar açılı üçgen
Üç açısının ölçüsü de 90° den küçük olan üçgenlere dar açılı üçgen denir. |
|
b. Dik açılı üçgen
Bir açısının ölçüsü 90°’ye eşit olan üçgenlere denir. Dik üçgen olarak adlandırılır. |
|
c. Geniş açılı üçgen
Bir açısının ölçüsü 90° den büyük olan üçgenlere denir. Bir üçgende bir tek geniş açı olabilir. |
|
Üçgenin kenarlarına ve açılarına temel elemanlar, yükseklik, kenarortay ve açıortaylarına yardımcı elemanlar denir.
1. Yükseklik
Bir köşeden karşı kenara veya karşı kenarın uzantısına çizilen dik doğru parçasına yükseklik denir.
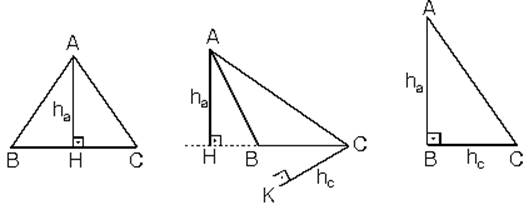 |
ha ® a kanarına ait yükseklik. |
2. Açıortay
Üçgenin bir köşesindeki açıyı iki eş parçaya ayıran ışına o köşenin açıortayı denir.
nA ® A köşesine ait iç açıortay n'A ® A köşesine ait dış açıortay |
|
3. Kenarortay
Üçgenin bir kenarının orta noktasını karşısındaki köşe ile birleştiren doğru parçasına o kenara ait kenarortay denir. |AD| = Va , |BE| = Vb olarak ifade edilir. |
|
Dik üçgende, dik köşeden çizilen yani hipotenüse ait kenarortay hipotenüsün yarısına eşittir. |
|