ÜÇGENDE AÇI ÖZELLİKLERİ

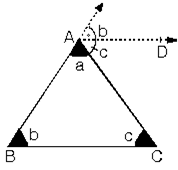
1. Üçgende iç açıların ölçüleri toplamı 180° dir.

[AD // [BC] olduğundan,

İç ters (c) ve yöndeş (b) olan açıları şekil üzerinde gösterirsek. a + b + c = 180°

m(A) + m(B) + m(C) = 180°

Üçgenin iç açılarının toplamı 180° dir. İç açılara komşu ve bütünler olan açılara dış açı denir.

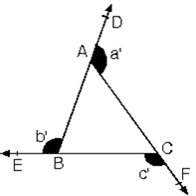
2. Üçgende dış açıların ölçüleri toplamı360° dir.

a' + b' + c' = 360°

m(DAF)+m(ABE)+m(BCF)=360°

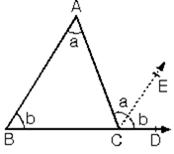
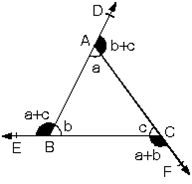
3. Üçgende bir dış açının ölçüsü kendisine komşu olmayan iki iç açının ölçüleri toplamına eşittir.

[AB] // [CE olduğundan

İç ters açıları a, yöndeş açıları b ile gösterirsek;

m(ACD)=a+b

m(DAC) = m(A') = b + c

m(DBE) = m(B') = a + c

m(ECF) = m(C') = a + b

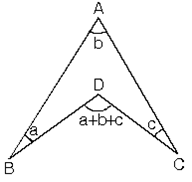
Yandaki şekilde a, b, c bulundukları açıların ölçüleri ise,

m(BDC) = a+b+c

4. İki kenarı eş olan üçgene ikizkenar üçgen denir. ABC üçgeninde:

 lABl=lACl m(B)=m(C)

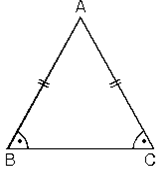
Burada A açısına (eşit kenarların birleştiği noktada oluşan açı)  ikizkenar üçgenin tepe açısı, A açısının gördüğü [BC] kenarına ise tabanı denir. Tepe açısına m(BAC) = α dersek

Taban açıları

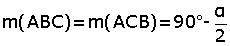
5. Üç kenarı eş olan üçgene eşkenar üçgen denir.

ABC üçgeninde

|AB| = |BC| = |AC|

m(A) = m(B) = m(C) = 60°

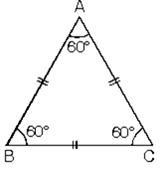
Eşkenar üçgen, ikizkenar üçgenin bütün özelliklerini taşır. 

ÜÇGENDE AÇIORTAYLAR

1. Üçgende iç açıortaylar bir noktada kesişirler. Bu nokta üçgenin iç teğet çemberinin merkezidir. Genelde I ile gösterilir.

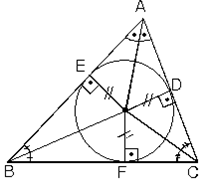
Açıortayların kesiştiği noktadan kenarlara çizilen dikmelerin uzunlukları eşittir. (Çemberin yarıçapı)

2. Üçgende iki dış açıortay ile üçüncü iç açıortay bir noktada kesişirler. Bu nokta üçgenin dıştan teğet çemberlerinden birinin merkezidir. (Üç tane dış teğet çember vardır.)

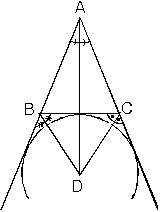
[AD], [BD] ve [CD] açıortaylarından herhangi ikisi verildiğinde üçüncüsü de kesinlikle açıortaydır.

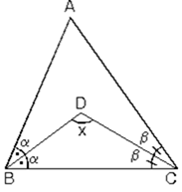
3. İki iç açıortayın kesişmesiyle oluşan açı; ABC üçgeninde ve BDC üçgeninde iç açılar toplamı  yazılırsa aşağıdaki formül bulunur: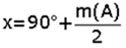

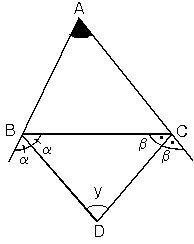
4. İki dış açıortayın kesişmesiyle oluşan açı; ABC üçgeninin dış açılar toplamı ve BDC üçgeninin iç açılar toplamını yazarsak aşağıdaki formül bulunur: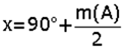 

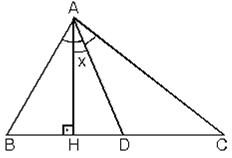
5. Bir iç açıortay ile bir dış açıortayın kesişmesiyle oluşan açı,

ABC üçgeninin C açısının dış açıortayı ile B açısının iç açıortayı arasındaki açının ölçüsü A açısının ölçüsünün yarısıdır.

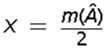
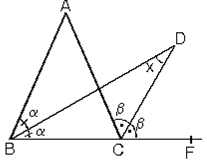
Burada D noktası dış teğet çemberlerden birinin merkezi olduğundan, A dan çizilen dış açıortayda D noktasından geçer.

6. Açıortayla yükseklik arasında kalan açı; ABC üçgeninde [AD] A açısına ait açıortay ve [AH] yüksekliktir. Açıortayla yükseklik arasındaki açıya 

m(HAD) = x dersek

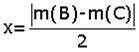
Bir açı ve açıortayını başka bir doğrunun kestiği durumlarda dış açı özelliği kullanılarak bütün açılar bulunabilir.