Düzgün Doğrusal Hareket Bir hareketlinin doğrusal bir yol boyunca eşit zaman aralıklarında eşit yollar almasına denir. Sabit hızlı harekette ivme sıfırdır(a=0). Çünkü hızda herhangi bir artış ya da azalış olmaz.
Düzgün doğrusal hareket grafikleri;
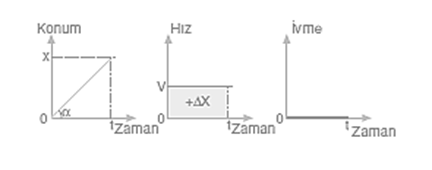
Konum zaman grafiği eğimi hızı verdiği için cismin konum zaman grafiği eğimi sabittir. Hızın sabit olmasından dolayı hız zaman grafiği eğimi sıfırdır.
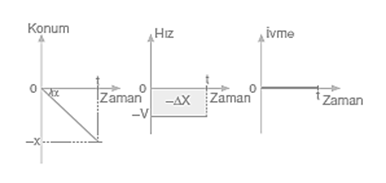
Konum zaman grafiği eğimi hızı verdiği için cismin konum zaman grafiği eğimi sabittir. Hızın sabit olmasından dolayı hız zaman grafiği eğimi sıfırdır.
Sabit İvmeli Hareket Bir hareketlinin eşit zaman aralıklarında hızını sabit olarak artırmasına ya da azaltmasına denir.
Bir cismin sabit ivme ile hızlanmasına denir. Düzgün hızlanan hareket grafikleri;
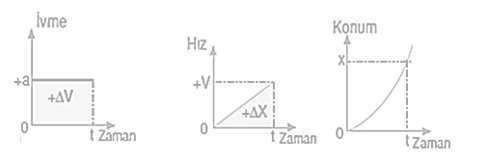
İvme zaman grafiği altında kalan alan yardımı ile hız değişimi; ∆V=a.t olarak hesaplanır. Konum zaman grafiği eğimi hızı verdiği için hızlanan cismin konum zaman grafiği eğimi giderek artmaktadır.
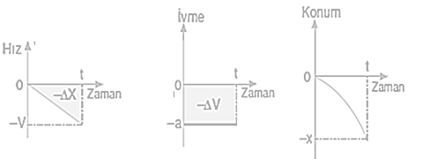
İvme zaman grafiği altında kalan alan yardımı ile hız değişimi; -∆V=-a.t olarak hesaplanır. Konum zaman grafiği eğimi hızı verdiği için hızlanan cismin konum zaman grafiği eğimi giderek artmaktadır.
Düzgün yavaşlayan hareket grafikleri;
Bir cismin sabit ivme ile yavaşlamasına denir. Düzgün yavaşlayan hareket grafikleri
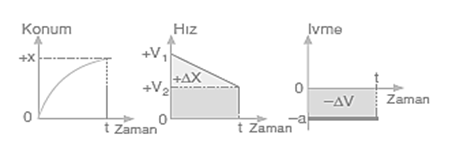
Konum zaman grafiği eğimi hızı verdiği için yavaşlayan cismin konum zaman grafiği eğimi giderek azalmaktadır.
Cismin ilk hızı V1 zamanla düzgün azalarak t sure sonunda V2 olmaktadır.
V2 – V1 = -∆V
İvme zaman grafiği yardımı ile hız değişimi;
-∆V=-a.t olarak hesaplanır.
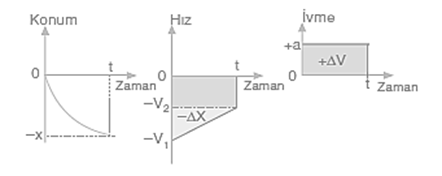
Konum zaman grafiği eğimi hızı verdiği için yavaşlayan cismin konum zaman grafiği eğimi giderek azalmaktadır.
Cismin ilk hızı -V1 zamanla düzgün azalarak t sure sonunda- V2 olmaktadır.
-V2 – (-V1) = ∆V İvme zaman grafiği yardımı ile hız değişimi;
∆V=-a.t olarak hesaplanır.