TÜREVİN GEOMETRİK YORUMU
TEĞET DENKLEMİ

 eğrisinin  noktasındaki teğetinin eğimi,  fonksiyonunun  noktasındaki türevine eşittir.
ÖRNEK:  fonksiyonun  noktasındaki teğetin eğimini bulalım.
ÇÖZÜM:   olarak bulunur.

ARTAN VE AZALAN FONKSİYONLAR
 fonksiyonu türevli olsun.   için;  ise  fonksiyonu  aralığında artan,  ise  fonksiyonu  aralığında azalandır.
ÖRNEK:  fonksiyonunun artan ve azalan olduğu aralıkları bulalım.
ÇÖZÜM:   

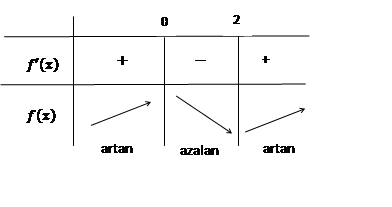
Artan olduğu aralık:       azalan olduğu aralık:
EKSTREMUM NOKTA:
 fonksiyonu için,  yapan   noktasına kritik nokta denir.
Her  sayısı için  ise  noktasına  fonksiyonun yerel (bağıl) maksimum değeri denir.
Her  sayısı için  ise  noktasına  fonksiyonun yerel (bağıl) minumum değeri denir.
ÖRNEK:  fonksiyonu inceleyelim.
ÇÖZÜM:   

0 noktası yerel maksimum, 2 noktası yerel minumumudur.
 
Yerel maksimum noktası:                   Yerel maksimum noktası:

MAKSİMUM VE MİNUMUM PROBLEMLERİ
Bu tarz problemleri çözerken istenilen ifadeyi tek değişkene göre yazıp istenilen ifadenin türevini alıp sıfıra eşitlendiğinde bulunan değer istenilen bulunur.
ÖRNEK:  olduğuna göre,  çarpımının alabileceği en küçük değeri bulalım.
ÇÖZÜM:   bulunan en son ifadenin türevini alıp sıfıra eşitleyelim.
 değeri için en küçük değeri alır.     olur.
 olarak bulunur.
İKİNCİ TÜREVİN GEOMETRİK YORUMU
 fonksiyonu  aralığında sürekli ve iki kere türev alınabilen fonksiyon olsun. Her   için  sağlanıyorsa bu aralıkta fonksiyon konkav, her   için  sağlanıyorsa bu aralıkta fonksiyon konvekstir.
İkinci türevi sıfır yapan değer ise fonksiyonun dönüm noktasıdır.
ÖRNEK:  fonksiyonunun ikinci türevini inceleyelim.
ÇÖZÜM:
 
 bulunan bu değerler dönüm noktasıdır.

ASİMPTOTLAR
 iken bir noktada soldan veya sağdan limit değerleri artı ve ya eksi sonsuza giderse fonksiyonun bu noktada düşey asimptotu vardır denir.
Fonksiyonda değişken artı veya eksi sonsuza giderken limiti bir reel sayıya eşit olursa bu fonksiyonun yatay asimptotu vardır denir.