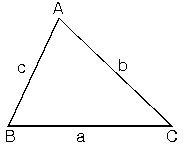
1. Bir üçgende ölçüsü büyük olan açının karşısındaki kenar uzunluğu, ölçüsü küçük olan açının karşısındaki kenar uzunluğundan daha büyüktür. Yani büyük açı karşısında büyük kenar, küçük açı karşısında küçük kenar bulunur.
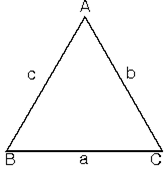
ABC üçgeninde m(A) > m(B) > m(C)
a > b > c
Terside geçerlidir. Uzun kenarı gören açı kısa kenarı gören açıdan daha büyüktür. İkizkenar üçgenden de bildiğimiz gibi eşit açıların karşılarındaki kenarlar eşittir.
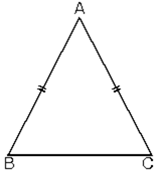
m(B) = m(C) => |AB| = |AC|
m(A) < m(B) = m(C) ise
|BC| < |AB| = |AC| olur.
Bir üçgende bir tane geniş açı olabileceğinden geniş açının karşısındaki kenar daima en büyük kenar olur.
2. Bir üçgende herhangi bir kenarın uzunluğu diğer iki kenarın uzunlukları toplamından küçük farkının mutlak değerinden büyüktür. ABC üçgeninde,
│b - c l <a < (b + c)
Diğer kenarlar için de aynı durum geçerlidir.
|a – c| < b < (a + c) ve |a – b| < c < (a + b) olur.
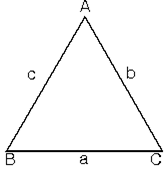
3. Dik, dar ve geniş açılı üçgenlerde kenarlar arasındaki ilişkiler.
a. Bir dik üçgende kenarlar arasında Pisagor Teoremi a2 = b2 + c2 bağıntısı vardır.
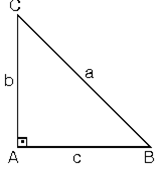
b. Dar açılı üçgende b ve c sabit tutulup A açısı küçültülürse a da küçülür.
m(A) < 90° a2 < b2 + c2
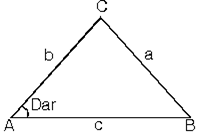
c. Geniş açılı üçgende b ve c sabit tutulup A açısı büyütülürse a da büyür.
m(A) < 90° a2 > b2 + c2
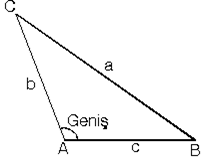
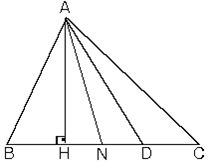
4. Çeşitkenar bir üçgende aynı köşeden çizilen yükseklik, açıortay ve kenarortay uzunluklarının sıralanması,
|AH| = ha ; yükseklik
|AN| = nA ; açıortay
|AD| = Va ; kenarortay
Olmak üzere; ha< nA <Va şeklinde sıralama vardır.
5. Çeşitkenar bir üçgende, açı, açıortay, kenarortay ve yükseklik arasındaki sıralama; ABC üçgeninde a, b, c kenar uzunluklarıdır.
m(A) > m(B) > m(C) olduğunu varsayalım. Bu durumda üçgende
Kenarlar : a > b > c
Yükseklikler : ha < hb < hc
Açıortaylar : nA < nB < nC
Kenarortaylar : Va < Vb < Vc
şeklinde sıralanırlar. Yani üçgenin yardımcı elemanları kenarlarının sırasına ters yönde sıralanır. Eşkenar ve ikizkenar üçgen için bu sıralamalar geçerli değildir.
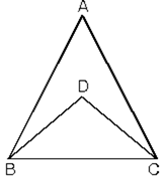
6. Bir kenarları ortak olan iç içe iki üçgenden içtekinin çevresi daha küçük olur.
|BD| + |DC| < |AB| + |AC|
ABCD bir dörtgen, a, b, c, d kenar uzunlukları [AC] ve [BD] köşegenlerdir. ABCD dörtgeninde karşılıklı kenarların uzunlukları toplamı, köşegenlerin uzunlukları toplamından küçüktür.
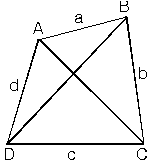
a + c < |AC| + |BD| ve b + d < |AC| + |BD|
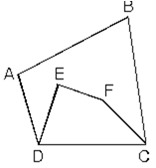
Köşegen uzunlukları toplamı çevreden daha büyük ve çevrenin yarısından daha küçük olamaz. İç içe şekillerde içteki şeklin çevresi daha küçük olacağından
|DA| + |AB| + |BC| toplamı |DE| + |EF| + |FC| toplamından daha büyüktür.
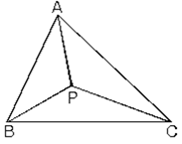
7. ABC üçgeninin içindeki herhangi bir P noktası için; |AP| + |BP| + |CP| toplamı ABC üçgeninin en büyük iki kenarının toplamından büyük, çevresinin yarısından küçük olamaz.