D. Aritmetik Ortalama
Bu sayıların toplamının n ile bölümüne aritmetik ortalama denir. Bunun formülü,
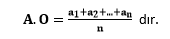
O halde, aritmetik ortalamaya x dersek, x . n = sayıların toplamı denklemini oluşturabiliriz.
E. Geometrik Ortalama

bu sayıların çarpımının n. Dereceden kuvvetten köküne geometrik ortalama denir. Bunun formülü;
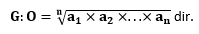
F. Harmonik Ortalama

n sayısının bu n tane sayının çarpmaya göre terslerinin toplanması ile elde edilen değere oranlanmasına harmonik ortalama denir.Bunun formülü,
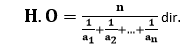
NOT: a ile b birbirine eşit sayılar ise, bu iki sayının aritmetik ortalaması, geometrik ortalaması ve harmonik ortalaması birbirine eşittir.
KONU DEĞERLENDİRME SORULARI
1. a, b, c pozitif sayılardır. a . b = 3 , a . c = 5 , b . c = 7 olduğuna göre bu sayıları küçükten büyüğe sıralayınız.
Cevap: c > b > a

2. Bir usta bir evi 6 günde boyuyor. Boyanan her eve bir aile taşınıyor. Usta sayısı 3 katına çıkartılırsa 20 günde kaç aile taşınmış olur?
Cevap: 10
Burada usta sayısı, bayama günü ile ters orantılıyken taşınan aile sayısı ile doğru orantılıdır. O halde, bileşik oran formülünden,
(Usta Sayısı / Taşınan Aile Sayısı) . Boyama Yapılan Gün Sayısı = k denklemini kurabiliriz. Bizden istenen taşınan aile sayısını bilmediğimiz için a olarak adlandıralım. Bu durumda,
k = (Usta Sayısı / Taşınan Aile Sayısı) . Boyama Yapılan Gün Sayısı = (1 / 1) . 6 = 6 = (3 / a) . 20 dir.Böylece a = 10 bulunur.
3. a ve b sayılarının aritmetik ortalaması 10 , geometrik ortalaması 5 √3 olduğuna göre , a² + b² ifadesi kaçtır?
Cevap: 250
A.O = (a + b) / 2 = 10 olduğundan a + b = 20 dir.
G.O = √a . √b = 5√3 olduğundan a . b = 75 dir.
(a + b)² = a² + 2 . a . b + b² olduğundan 400 = a² + 2. 75 + b² dir. O halde, a² + b² = 250 elde edilir.