ORAN - ORANTI
A. Tanım
Aynı türden iki ifadenin birbiriyle kıyaslanmalarına oran denir. Birden fazla oranın birbirine eşitlenmesine orantı denir. Orantılar genellikle k sabitine eşitlenir.
- a,b,c,d ∈ R olmak üzere;
a/b ve c/d oran kavramına örnekken, a/b = c/d = k orantı kavramına örnektir.
B. Orantının Özellikleri
1. a/b = c/d ise , a . d = b . c
2. a/b = c/d ise , d/b = c/a
a/c = b/d
c/d = a/b eşitlikleri yazılabilir.
3. a/b = c/d = e/f = k ise , (a + c + e) /(b + d + f) = k'dır.
4. m,n ∈ R olmak üzere,
a/b = c/d = k ise,
* (m . a) / (m . b) = (n . c) / (n . d) = k'dır.
* (m . a) + (n . c) / (m . b) + (n . d) = k'dır.
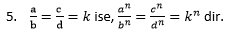
6. a/b = c/d = k ise, a/b = c/d = k² dir.
7. a:b:c = x:y:z ise , a/x = b/y = c/z = k dır.
8. a/x = b/y = c/z = k ise , a = x . k , b = y . k , c = z . k dır.
C. Orantı Çeşitleri
1. Doğru Orantı
Aralarında orantı olan iki çokluktan biri artarken(azalırken) diğeri de artarsa(azalırsa) bu iki çokluk doğru orantılıdır. x ve y doğru orantılı olmak üzere, x = k . y doğru orantı denklemidir.
Örnek: Garson sayısı arttıkça servis hızının artması.
Bir fabrikadaki makine sayısı arttıkça üretilen ürün sayısının artması.
2. Ters Orantı
Aralarında orantı olan iki çokluktan biri artarken(azalırken) diğeri de azalırsa (artarsa) bu iki çokluk ters orantılıdır . x ve y doğru orantılı olmak üzere, x = y / k ters orantı denklemidir.
Örnek: Bir inşaattaki usta sayısı arttıkça kişi başına düşen işin azalması.
Musluk sayısı arttıkça bir havuzun dolma süresinin azalması.
3. Bileşik Orantı
Birden fazla oran içeren orantılara bileşik orantı denir.
a : b : c = x : y : z
a/x = b/y = c/z = k dır.
a . x = b . y = c . z = k dır.