ORAN - ORANTI
a'nın b'ye oranı; a:b veya a/b şeklinde gösterilir. b ≠ 0 olmalıdır.
İki veya daha fazla oranın eşitlenmesiyle oluşan ifadeye orantı denir.
a/b = c/d = k ifadesine orantı;k'ya orantı sabiti denir.

y/x = k → x ve y doğru orantılıdır.
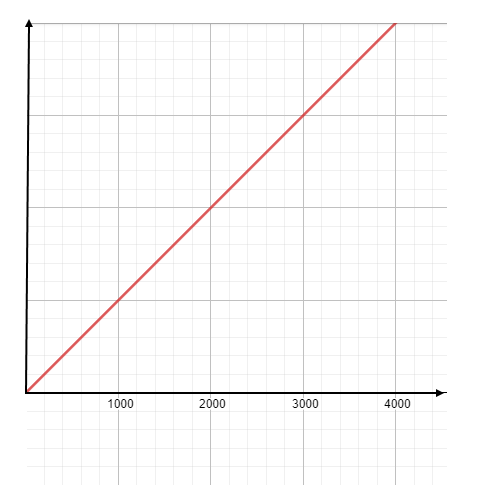
x . y = k → x ve y ters orantılıdır.
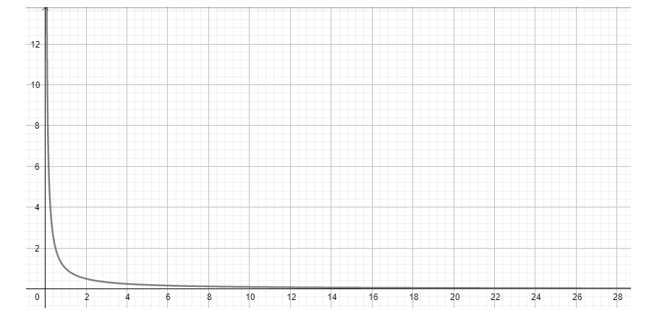
ÇÖZÜMLÜ ÖRNEKLER
1) a sayısı b ile doğru , c ile ters orantılıdır.
b = 5 , c = 8 ise a = 9 olur.
Buna göre,= 25 , c = 72 ise a değerini bulunuz.
ÇÖZÜM: a = k . (b/c) olur. b = 5, c = 8 ve a = 9 ise,
9 = k . (5/8) ⇒ k = 72 / 5 olur.
b = 25 ve c = 72 iken a = (72/5) . (25/72) = 5 bulunur.
2) x , y , z sayıları 2,5,7 sayıları ile orantılıdır.
5x - y + z = 144 olduğuna göre x değeri kaçtır?
ÇÖZÜM: x = 2k , y = 5k , z = 7k (doğru orantı)
10k - 5k + 7k = 144 ⇒ 12k = 144
⇒ k = 12
⇒ x = 24
3) 185 m² lik bir arazi 3 ile doğru orantılı, 2 ve 5 ile ters orantılı olarak üç parçaya ayrılmıştır. Buna göre, en büyük parça kaç
m² olmalıdır?
ÇÖZÜM: Parçalar, 3k , k/2 ve k/5 olmalıdır.
3k + k/2 + k/5 = 185 ⇒ (30k + 5k + 2k) / 10 = 185
⇒ 37k = 1850
⇒ k = 50
En büyük parça, 3k = 3 . 50 = 150 m² 'dir.