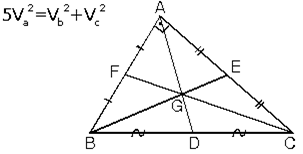
3. Kenarortayların Böldüğü Alanlar
a.Kenarortaylar üçgenin alanını altı eşit parçaya bölerler.
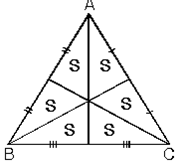
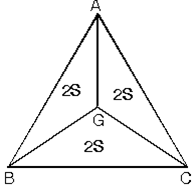
b.G ağırlık merkezi köşelere birleştirildiğinde üçgenin alanı üç eşit parçaya bölünür.
c. G ağırlık merkezi kenarların orta noktaları ile birleştirildiğinde üçgenin alanı üç eşit parçaya bölünür.
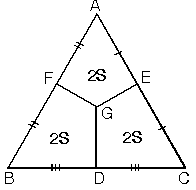
4.ABC üçgeninde kenarortaylar ve orta taban [FE] çizilirse
|AK| = 3x
|KG| = x
|GD| = 2x eşitlikleri bulunur.
Buna kısaca 312 kuralı denebilir.
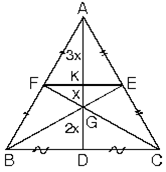
K noktası [AD] kenarortayının orta noktasıdır. Ayrıca [FE] orta taban olduğundan;
[FE] // [BC] 2[FE]=[BC]
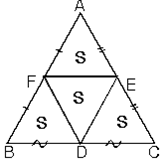
a. ABC üçgeninde kenarortaylar ve [FE] çizildiğinde şekildeki gibi bir alan bölünmesi oluşur.

b.Kenarların orta noktalarını birbirine birleştirdiğimizde üçgenin alanı dört eşit parçaya bölünür.
5. Kenarortay Uzunluğu (Kenarortay Teoremi). ABC üçgeninde A köşesinden çizilen kenarortayın uzunluğuna Va dersek
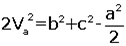
Bu bağıntı diğer kenarortaylar içinde geçerlidir.
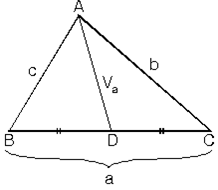
Kenarortaylar taraf tarafa toplanırsa
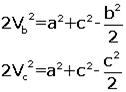
Kenarortaylar taraf tarafa toplanırsa
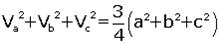
elde edilir.
6. Dik Üçgende Kenarortaylar. A açısı 90° olan bir dik üçgende kenarortaylar arasında