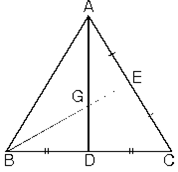
1. Ağırlık Merkezi. Üçgenlerde kenarortaylar bir noktada kesişirler. Kenarortayların kesişim noktasına ağırlık merkezi denir. ABC üçgeninde [AD], [BE] ve [CF] kenarortaylarının kesiştikleri G noktasına ABC üçgeninin ağırlık merkezi denir.

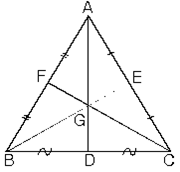
a. Ağırlık merkezi kenarortayı, kenara 1 birim, köşeye 2 birim uzaklık olacak şekilde böler. ABC üçgeninde D, E, F noktaları bulundukları kenarların orta noktaları ve G ağırlık merkezi ise

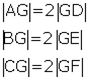
eşitlikleri vardır.

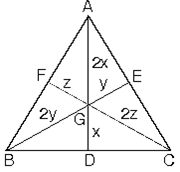
b. Bir üçgende iki kenarortayın kesişmesiyle oluşan nokta ağırlık merkezidir.

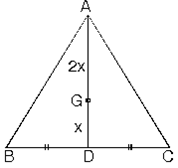
c. ABC üçgeninde [AD] kenarortay ve |AG| = 2|GD| olduğunda G noktası ağırlık merkezidir.

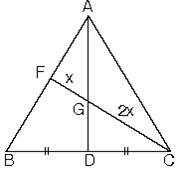
d. ABC üçgeninde [AD] kenarortay ve |CG| = 2|FG| olduğunda G noktası ağırlık merkezidir.

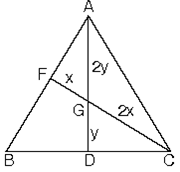
e. ABC üçgeninde |AG| = 2|GD| ve |CG| = 2|GF|eşitliğini sağlayan G noktası ABC üçgeninin ağırlık merkezidir.

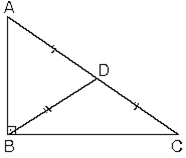
2. Dik üçgende hipotenüse ait kenarortay (dik köşeden çizilen kenarortay) hipotenüsün yarısına eşittir. ABC dik üçgeninde [BD] hipotenüse ait kenarortay

|AD|=|DC|=|BD|