GAZ YASALARI:

Bu bölümde basınç, hacim, sıcaklık ve gaz miktarı arasındaki ilişkileri inceleyeceğiz. Özellikle, değişkenlerden ikisi sabitken, diğerlerinin birbirlerine nasıl bağlı olduklarını göreceğiz. Bu ilişkilerin hepsine birden basit gaz yasaları denir.

Basınç – Hacim İlişkisi: Boyle-Mariotte Kanunu

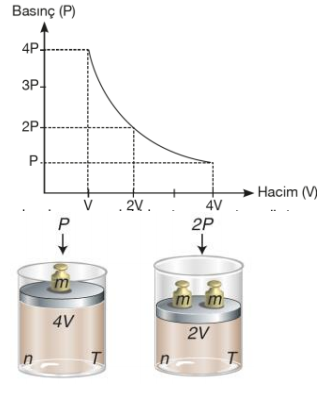
1662 yılında İngiliz kimyacı Robert Boyle gazların davranışını sistematik olarak ve nicel yönleriyle incelemiştir. Robert Boyle, çalışmalarında hava basıncının hacim üzerindeki etkilerini gözlemlemek için aşağıdaki gibi bir düzenek kurmuştur. Şekildeki gazı göz önüne alacak olursak bu gaz bir silindir içinde ve ağırlığı olmayan, serbestçe hareket edebilen bir piston ile kapatılmış olsun. Gaz basıncı piston üzerindeki toplam ağırlığa bağlıdır. Piston üzerindeki ağırlık 2 katına çıkarılırsa basınçta 2 katına çıkar ve gaz hacmi yarıya iner. Basınç ve hacim arasındaki bu ilişki aşağıdaki şekilde açıkça görülmektedir. Buna karşın eğer uygulanan basınç azaltılırsa, gazın hacmi artar. n ve T sabit olmak koşuluyla basınç ve hacim arasındaki bu ters orantıyı gösteren matematiksel ifade şöyledir.

P α 1/V ve P.V= k₁ k₁: Sabit bir sayı olup madde miktarı ve sıcaklığa bağlıdır. Verilen bir gaz örneği için, sıcaklık sabit tutulduğu ve gazın miktarı değişmediği sürece, basınç ve hacim değişmesine rağmen, P ile V nin çarpımı her zaman sabit bir değere eşittir. Böylece verilen gaz örneği için, sabit sıcaklıkta iki farklı koşul için, P₁V₁= k₁= P₂V₂ veya P₁V₁= P₂V₂ yazılabilir.

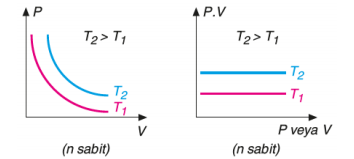
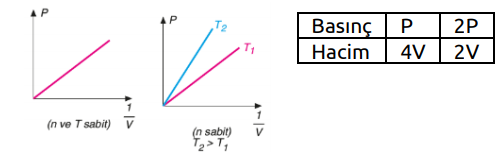
Farklı sıcaklıklarda eşit mole sahip olan bir gazın basınç (P) – hacim (V) değişimi ile basınç.hacim çarpımının (P.V)–basınç veya hacimle değişim grafikleri yukarıdaki gibidir.

Basınç 1/V değerine karşı grafiğe alındığında yukarıdaki grafikler elde edilir.

Hacim–Sıcaklık İlişkisi: Charles Kanunu Gazların hacimleri ile sıcaklıkları arasındaki ilişki ilk kez 1787 yılında Fransız fizikçi Jocques Charles tarafından keşfedilmiş ve bundan bağımsız olarak 1802 yılında başka bir Fransız fizikçi Joseph Gay Lussac tarafından yayınlanmıştır.

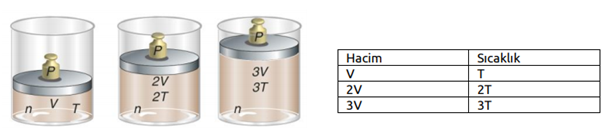
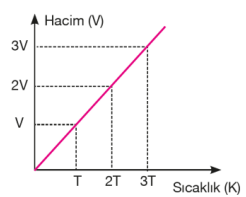
Yukarıdaki grafikte, bir gazın aynı basınç altında üç farklı sıcaklıktaki hacimlerinin değişimi gösterilmektedir. Buradan anlaşıldığı üzere gazın sıcaklığı arttıkça hacmi de artmaktadır. Gazın sıcaklığı düşürüldükçe hacmi küçülecek ve belirli bir sıcaklık değerinde sıvılaşmaya başlayacaktır. Sabit basınç altında ısıtılan bir gazın hacminin santigrat sıcaklığıyla ve kelvin sıcaklığı ile değişimi aşağıdaki grafiklerdeki gibidir.

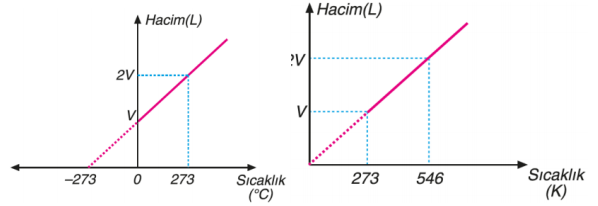
Kuramsal olarak ulaşılabilecek –273°C ye mutlak sıfır noktası veya mutlak sıcaklık adı verilir. Charles Yasasına göre sabit basınçta belirli miktar gazın hacmi, mutlak sıcaklığı ile doğru orantılıdır. T (Kelvin)= t °C + 273 Gaz hacminin sıcaklığa bağlılığı ise şu şekildedir. V α T ve V= k₂ . T k₂: Sabit bir sayı olup gazın basıncına ve miktarına bağlıdır. Sabit sıcaklıktaki basınç–hacim ilişkisinde olduğu gibi, sabit basınçtaki bir gaz örneğinin de iki farklı hacim-sıcaklık koşullarını karşılaştırabiliriz.

V₁ / T₁ = k₂ = V₁ / T₂

V₁ / T₁ = V₁ / T₂

Basınç-Sıcaklık İlişkisi: Gay–Lussac Kanun

Fransız bilim insanı Joseph Gay–Lussac yapmış olduğu çalışmalar sonucunda, Charles yasasına benzer bir ilişkinin madde miktarı (mol sayısı) ve hacmin sabit tutulduğunda, basınçla sıcaklık arasında da olduğunu söylemiştir. Sabit bir hacim ve sabit miktarda alınan bir gazın basınç ­sıcaklık (°C) grafiği şekilde verilmiştir.

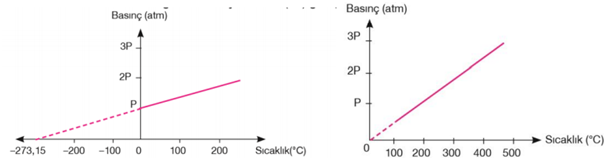
Aynı gazın basınç­ mutlak sıcaklık (K) grafiği çizildiğinde basınçla mutlak sıcaklık arasında doğru orantı olduğu görülür. Basınçla, mutlak sıcaklık arasında; P ∝ T veya P= k . T ifadesi yazılabilir. Burada "k" sabit olup, gazların miktarına ve hacmine bağlı olarak değişir. Yukarıdaki ifadeyi sabit hacim ve miktardaki farklı sıcaklık ve basınçlara sahip bir gaz örneği için; P₁ / T₁ = P₂ / T₂

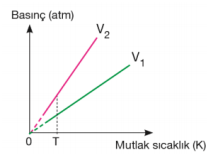
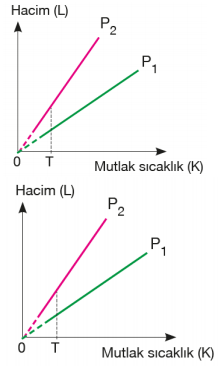
Basınç–mutlak sıcaklık grafiğindeki doğruların eğimlerinin karşılaştırılması; Mol sayısı sabitse eğim hacimler arasındaki ilişkiyi verir. Eğimi büyük olanın hacmi küçüktür. T sıcaklığında V₂ değerine gelen basınç daha büyük olduğu için hacmi daha küçüktür. V₁ > V₂

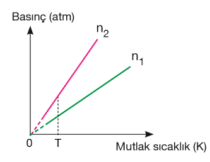
Hacim sabitse eğim mol sayıları arasındaki ilişkiyi verir. Eğimi büyük olanın mol sayısı da büyüktür. n₂ > n₁