
GAZ YASALARI Bu bölümde basınç, hacim, sıcaklık ve gaz miktarı arasındaki ilişkileri inceleyeceğiz. Özellikle, değişkenlerden ikisi sabitken, diğerlerinin birbirlerine nasıl bağlı olduklarını göreceğiz. Bu ilişkilerin hepsine birden basit gaz yasaları denir.

Basınç – Hacim İlişkisi: Boyle-Mariotte Kanunu 1662 yılında İngiliz kimyacı Robert Boyle gazların davranışını sistematik olarak ve nicel yönleriyle incelemiştir. Robert Boyle, çalışmalarında hava basıncının hacim üzerindeki etkilerini gözlemlemek için aşağıdaki gibi bir düzenek kurmuştur. Şekildeki gazı göz önüne alacak olursak bu gaz bir silindir içinde ve ağırlığı olmayan, serbestçe hareket edebilen bir piston ile kapatılmış olsun. Gaz basıncı piston üzerindeki toplam ağırlığa bağlıdır. Piston üzerindeki ağırlık 2 katına çıkarılırsa basınçta 2 katına çıkar ve gaz hacmi yarıya iner. Basınç ve hacim arasındaki bu ilişki aşağıdaki şekilde açıkça görülmektedir. Buna karşın eğer uygulanan basınç azaltılırsa, gazın hacmi artar. n ve T sabit olmak koşuluyla basınç ve hacim arasındaki bu ters orantıyı gösteren matematiksel ifade şöyledir.

Pα 1/V ve P.V= k1 k1: Sabit bir sayı olup madde miktarı ve sıcaklığa bağlıdır. Verilen bir gaz örneği için, sıcaklık sabit tutulduğu ve gazın miktarı değişmediği sürece, basınç ve hacim değişmesine rağmen, P ile V nin çarpımı her zaman sabit bir değere eşittir. Böylece verilen gaz örneği için, sabit sıcaklıkta iki farklı koşul için, P1V1= k1= P2V2 veya P1V1= P2V2 yazılabilir.

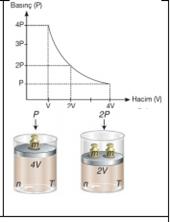
Farklı sıcaklıklarda eşit mole sahip olan bir gazın basınç (P) – hacim (V) değişimi ile basınç .hacim çarpımının (P.V)–basınç veya hacimle değişim grafikleri yukarıdaki gibidir. Basınç 1/V değerine karşı grafiğe alındığında yukarıdaki grafikler elde edilir. Özet: Sabit sıcaklıkta belli miktar gazın basıncı ile hacmi ters orantılıdır. Bu kanunla n ve T sabit iken P - V ilişkisi ortaya konmuştur. Buna göre sıcaklık ve mol sayısı eşitken iki gaz için hacim ve basınç çarpımı birbirine eşittir.
Yani P1.V1 = P2.V2 olur.
Hacim–Sıcaklık İlişkisi: Charles Kanunu Gazların hacimleri ile sıcaklıkları arasındaki ilişki ilk kez 1787 yılında Fransız fizikçi Jocques Charles tarafından keşfedilmiş ve bundan bağımsız olarak 1802 yılında başka bir Fransız fizikçi Joseph Gay Lussac tarafından yayınlanmıştır.
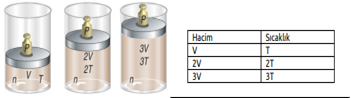
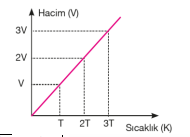
Yukarıdaki grafikte, bir gazın aynı basınç altında üç farklı sıcaklıktaki hacimlerinin değişimi gösterilmektedir. Buradan anlaşıldığı üzere gazın sıcaklığı arttıkça hacmi de artmaktadır. Gazın sıcaklığı düşürüldükçe hacmi küçülecek ve belirli bir sıcaklık değerinde sıvılaşmaya başlayacaktır. Sabit basınç altında ısıtılan bir gazın hacminin santigrat sıcaklığıyla ve kelvin sıcaklığı ile değişimi aşağıdaki grafiklerdeki gibidir.
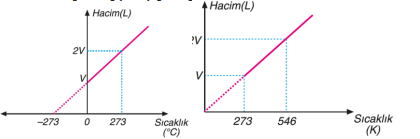
Kuramsal olarak ulaşılabilecek –273°C ye mutlak sıfır noktası veya mutlak sıcaklık adı verilir. Charles Yasasına göre sabit basınçta belirli miktar gazın hacmi, mutlak sıcaklığı ile doğru orantılıdır. T (Kelvin)= t °C + 273 Gaz hacminin sıcaklığa bağlılığı ise şu şekildedir. V α T ve V= k2. T k2: Sabit bir sayı olup gazın basıncına ve miktarına bağlıdır. Sabit sıcaklıktaki basınç–hacim ilişkisinde olduğu gibi, sabit basınçtaki bir gaz örneğinin de iki farklı hacim-sıcaklık koşullarını karşılaştırabiliriz.
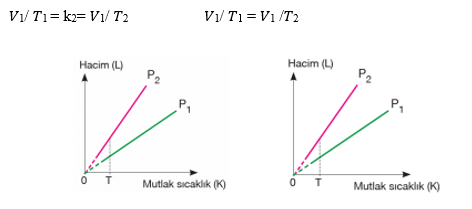
Özet: n ve P sabit iken V - T ilişkisi ortaya konmuştur. Sabit basınç altında ideal pistonlu bir kapta bulunan bir miktar gazın mutlak sıcaklığı ile hacmi doğru orantılıdır. Bunu iki gaz için bir eşitliğe dökersek mol sayısı ve basınç aynı iken
V1/T1 = V2/T2 olur.
Basınç-Sıcaklık İlişkisi: Gay–Lussac Kanun
Basınç – Sıcaklık İlişkisi: Gay - Lussac Kanunu Fransız bilim insanı Joseph Gay–Lussac yapmış olduğu çalışmalar sonucunda, Charles yasasına benzer bir ilişkinin madde miktarı (mol sayısı) ve hacmin sabit tutulduğunda, basınçla sıcaklık arasında da olduğunu söylemiştir. Sabit bir hacim ve sabit miktarda alınan bir gazın basınç sıcaklık (°C) grafiği şekilde verilmiştir.
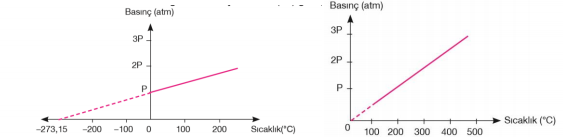
Aynı gazın basınç mutlak sıcaklık (K) grafiği çizildiğinde basınçla mutlak sıcaklık arasında doğru orantı olduğu görülür. Basınçla, mutlak sıcaklık arasında; P ∝ T veya P= k . T ifadesi yazılabilir. Burada "k" sabit olup, gazların miktarına ve hacmine bağlı olarak değişir. Yukarıdaki ifadeyi sabit hacim ve miktardaki farklı sıcaklık ve basınçlara sahip bir gaz örneği

şeklinde yazabiliriz.
Basınç–mutlak sıcaklık grafiğindeki doğruların eğimlerinin karşılaştırılması; Mol sayısı sabitse eğim hacimler arasındaki ilişkiyi verir. Eğimi büyük olanın hacmi küçüktür. T sıcaklığında V2 değerine gelen basınç daha büyük olduğu için hacmi daha küçüktür. V1 > V2
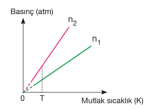
Hacim sabitse eğim mol sayıları arasındaki ilişkiyi verir. Eğimi büyük olanın mol sayısı da büyüktür. n2 > n1
Özet: V ve n sabit iken T - P ilişkisi ortaya konmuştur. Sabit hacimli bir kapta bulunan bir miktar ideal gazın basıncı ile mutlak sıcaklığı doğru orantılıdır. Yani P1/T1 = P2/T2 olur. Burada basınç ve sıcaklığın doğru orantılı olduğu da kolaylıkla görülür.
Mol Sayısı–Hacim İlişkisi Avogadro Kanunu Miktarı artırılan bir gazın basıncı ve sıcaklığı sabit ise hacminde bir artış olur. Yani hacimdeki değişim miktarı, molekül sayısındaki değişim ile doğru orantılıdır. Bu oran V a n veya V= k.n (k= sabit) şeklinde ifade edilebilir. Bir gazın iki farklı hacim ve miktarı arasındaki ilişki ise;
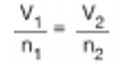
şeklinde ifade edilir. Deneyler Normal Koşullarda, NK’da (0°C ve 1 atm basınçta) 1 mol (6,02.1023 tanecik) ideal gazın 22,4 litre hacim kapladığını göstermiştir.
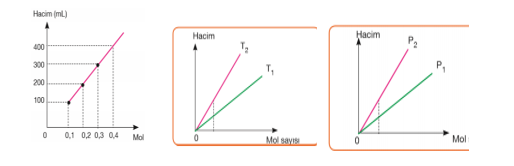
Hacim–mol sayısı grafiğindeki doğruların eğimlerinin karşılaştırılması; Basınç sabitse eğim mutlak sıcaklıklar arasındaki ilişkiyi verir. Eğimi büyük olanın mutlak sıcaklığı büyüktür. T2 > T1
Mutlak sıcaklık sabitse eğim basınçlar arasındaki ilişkiyi verir. Eğimi büyük olanın basıncı küçüktür. P1 > P2
Özet: P ve T sabit iken n - V ilişkisi ortaya konmuştur. Aynı koşullarda (sabit sıcaklık ve basınçta) bulunan gazların hacimleri mol sayısı ile doğru orantılıdır. Bu hipoteze göre sabit basınç ve sıcaklık varken iki gaz için V1/n1 = V2/n2 eşitliği elde edilir.

Mol Sayısı – Basınç İlişkisi
Dalton'un Kısmi Basınçlar Kanunu İdeal gaz kanunu tek tek gazlara uygulandığı gibi birbirleriyle etkileşmeyen gaz karışımlarına da uygulanabilir. Gazların kısmi basıncı John Dalton tarafından incelenmiştir.
Sabit hacimli kapalı bir kapta sabit sıcaklıkta bulunan gaz karışımının kaba yaptığı basınca toplam basınç, gazlardan birinin kaba yaptığı basınca o gazın kısmi basıncı denir.
Kısmi basınç problemlerinde aynı ortam geçerli oldu için hacim ve sıcaklık aynı olacaktır. Dolayısıyla gazların mol sayıları basınçları ile doğru orantılı olur.
Örneğin bir kapta 3 mol X gazı ve 2 mol Y gazı olsun. Bu durumda toplam basıncın 10 Atm olduğunu düşünürsek X gazının kısmi basıncı 6 Atm, Y gazının kısmi basıncı ise 4 Atm olur. Toplam basınç kısmi basınçların toplamıdır.
Sabit sıcaklık ve hacimde basınç ile mol sayısı doğru orantılı olarak değişir. Sabit hacimli kapta sabit sıcaklıkta mol sayısı arttıkça basınç da artar. Mol sayısı azaldıkça basınç da azalır. Bu oran P ∝ n veya P= k. n (k= sabit) şeklinde ifade edilebilir. Bir gazın iki farklı basınç ve
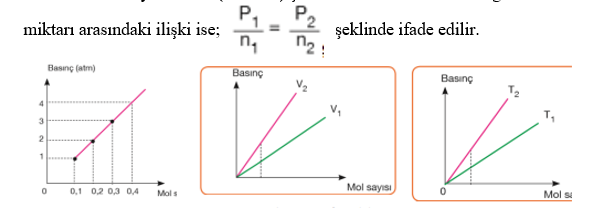
Basınç–mol sayısı grafiğindeki doğruların eğimlerinin karşılaştırılması; Sıcaklık sabitse eğim hacimler arasındaki ilişkiyi verir. Eğimi büyük olanın hacmi daha küçüktür. V1 > V2
Hacim sabitse eğim mutlak sıcaklıklar arasındaki ilişkiyi verir. Eğimi büyük olanın sıcaklığı daha fazladır. T2 > T1

İdeal Gaz Denklemi Gaz yasaları kullanılarak ideal gaz denklemi türetilir. Yukarıda verdiğimiz bütün hipotez ve kanunları birleştirsek elimize çok daha basit bir eşitlik gelecektir. Yukarıdaki verileri oranlığımız zaman;
P.V = n.R.T denklemi ortaya çıkar.
Bu denkleme ideal gaz denklemi denir. Buradaki R (Raydberg sabiti) bir sabittir ve 22,4 / 273 = 0,082 değerindedir. Basınç (P) birimi atm olmalıdır. Gazların hacmi (V) litre biriminden yazılmalıdır. Gazın sıcaklığı (T) kelvin cinsinden yazılmalıdır.

Birleşik Gaz Denklemi (Genel Gaz Denklemi) Bir gazın iki durumunu veya iki gazı karşılaştırmak için birleşik gaz denklemi kullanılır. İki ideal gaz denklemi birbirine orantılandığında birleşik gaz bağıntısı elde edilir. Hacim değişmeksizin ya da kapalı çelik bir kapta gibi ifadeler kullanılan sorularda formülden hacim sadeleştirilir.
Sabit sıcaklıkta ya da aynı sıcaklığa dönüldüğü gibi ifadelerinin kullanıldığı sorularda formülden sıcaklık sadeleştirilir.
Sabit basınçta ya da ideal pistonlu kapta ifadelerinin kullanıldığı sorularda formülden basınç sadeleştirilir.
Kısacası soruda sabit kabul edilen verilen formülden sadeleştirilir. Yukarıda ideal gaz denkleminde R diye bir sabitten bahsetmiştik. Bu sabit bütün ideal gazlar için aynı olduğundan denklemin bir tarafında yalnız bıraktığımızda genel gaz denklemini elde ederiz.
P1.V1/n1.T1 = P2.V2/n2.T2 = R formülünden bütün ideal gaz soruları çözülür. Sabit ya da eşit verilen değerleri denklemde sadeleştirebilir.

Gazların yoğunluğu ile ilgili uygulamalar için, ideal gaz denklemini yoğunluk niceliği ile beraber tekrar düzenleyebiliriz. Yoğunluğun kütlenin hacme bölümü olduğunu biliyoruz. Yani d = m/V maddenin bütün fazları için geçerlidir. Biz burada ideal gaz denklemi içine bu eşitliği yazarak yeni bir eşitlik elde edeceğiz. İdeal gazlar için geçerli olan formülde n mol sayısını veriyordu. Mol sayısı da her zaman n = m/MA ile bulunur. İdeal gaz denkleminde V yerine m/d, n yerine de m/MA yazarsak yeni bir bağıntı elde ederiz.
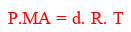
bağıntısı bu şekilde ortaya çıkar. Bazı sorularda mol kütlesi veya yoğunluk verildiğinde doğrudan bu formülü kullanabiliriz. Gazlarda hacim (V)'in birimi genellikle litre olduğundan yoğunluğu birim g/L'dir. Gazın yoğunluğu basınç, mutlak sıcaklık ve molekül ağırlığı ile değişebilir. Sabit hacimli kapta sıcaklık artırılırsa kabın hacmi ve kütlesi değişmediğinden yoğunluk değişmez.

Tanecikleri arasında etkileşimin olmadığı varsayılan ve taneciklerinin hacmi gazın kapladığı hacim yanında sıfır kabul edilen gazlar ideal gazlardır. Gerçekte ideal gaz yoktur. Ancak gerçek gazlar ideal hale yaklaşabilirler.

İdeal Gaz Denklemi: Basit gaz yasalarının üçü hacim değişikliklerine, diğer iki etkenin sabit kaldığı durumda, bir değişkenin etkisini anlatır. Boyle Mariotte kanunundan V ∝ 1/P ilişkisi, Charles kanunundan V ∝ T ilişkisi, Avogadro yasasından V ∝ n ilişkisi anlaşılmaktadır. Buna göre V ∝ n.T/P yazılabilir. R ile gösterilen ve ideal gaz sabiti olarak adlandırılan orantı kat sayısı kullanılarak P.V = n.R.T eşitliği elde edilir. Bu eşitliğe ideal gaz denklemi denir. İdeal gaz sabiti (R) = 22,4/273 veya 0,082 atm.L/mol.K dir.